¿Sabes qué relación guarda la ortogonalidad de vectores con el producto escalar, que significa ortogonal en vectores y qué son la ortogonalidad y ortonormalidad en productos vectoriales?
Ya hemos visto en nuestro post sobre la fórmula matemática del producto escalar que la fórmula del producto es la siguiente:
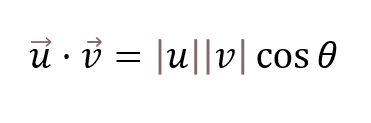
Ahora bien, esta fórmula nos da a entender que el producto escalar es la multiplicación de los módulos de los vectores por el ángulo que hacen entre ellos. Hemos visto, con esto, que el producto escalar es positivo, negativo o igual a cero:
- Producto > 0
- Producto < 0
- Producto = 0
Esto le abre paso al nuevo término, que es la ortogonalidad de vectores.
Ortogonalidad de vectores
La ortogonalidad de vectores viene definida cuando el producto escalar de dos vectores es cero:
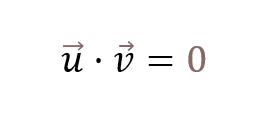
Esto quiere decir que si tenemos dos vectores y realizamos el producto escalar entre ellos y el resultado del producto escalar es 0, significa que los vectores son perpendiculares.
En matemáticas, en vez de decir que los vectores son perpendiculares, se dice que los vectores son ortocogonales.
Si el producto escalar es 0, pero además el módulo del vector u y el módulo del vector v son iguales a 1, es decir, tienen módulo unitario, son conjuntos ortonormales de vectores.
|u| = 1; |v| = 1 → vectores ortonormales
Ejemplo de vectores ortonormales
Veamos un ejemplo de vectores ortonormales, en este caso son los vectores unitarios.
Los vectores unitarios son vectores perpendiculares y su módulo es igual a 1. Vamos, pues, a calcular el producto escalar entre ambos vectores.
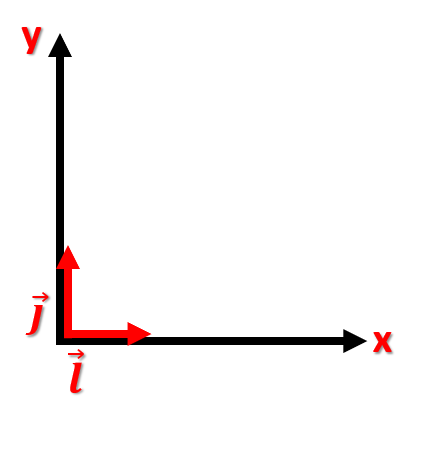
Tenemos el vector unitario en el eje x, que viene definido por 1 y 0, es decir, solo tiene componentes en el eje x:
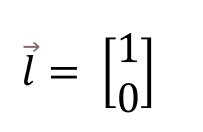
En cambio, el vector unitario en el eje y solo tiene componentes en el eje y:
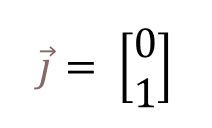
Vamos a hacer la prueba y el producto escalar. El producto escalar de y por x ya sabemos que es la multiplicación entre ellos.
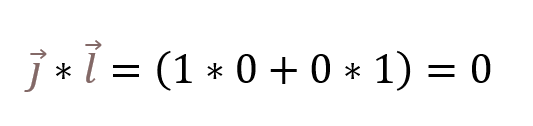
Ya sabemos que son perpendiculares, al menos hay una ortogonalidad. Pero, si calculamos el módulo de cada uno de ellos (el módulo no es más que su longitud), que se calcula usando el cuadrado del componente en el eje x más el cuadrado del componente en el eje y, el resultado debe dar 1. Esto se hace para el vector unitario l y el vector unitario j.
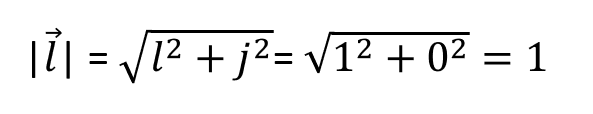
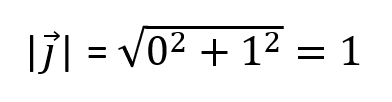
Ambos tienen módulo igual a 1, por tanto son ortonormales.
El Big Data es una de las áreas en las que más trabajos se ofertan. Si quieres ser uno de los afortunados que puede acceder a este tipo de opciones laborales, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos teóricos y prácticos que te permitirán lograr el trabajo de tus sueños. ¡No esperes más para seguir tu camino hacia el éxito y solicita información ahora!











