La razón de momios se define como el cociente entre dos probabilidades; su valor está en el rango [0, ∞].
Muchos sitios traducen el concepto del inglés odds ratio por razón de probabilidades, pero en realidad no es una probabilidad lo que está en juego, sino el ratio, como bien lo indica la palabra. El ratio se traduce a cómo de probable es respecto a cómo de no probable es. En este post aprenderás sobre la razón de momios.
¿En qué consiste la razón de momios?
A continuación verás cómo se puede definir la razón de momios y cómo calcular odds ratio.
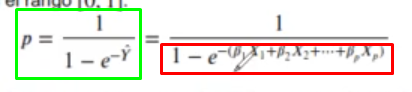
Tenemos un modelo de regresión lineal, señalada en el cuadro rojo, y le estamos aplicando la transformación señalada en el cuadro verde.
Si queremos calcular esto, ¿cómo lo podríamos resolver?
Pues podríamos dividir p entre 1 – p, el resultado, después de distintas operaciones, quedaría como el señalado en el recuadro azul, que representa la razón de momios y el resultado de calcular odds ratio:

Este resultado de calcular odds ratio es igual a la razón de momios o razón de odds.
Si aplicamos logaritmo a la izquierda y a la derecha, nos queda que el logaritmo de la razón de momios es igual a la regresión lineal.
Si aplicamos el logaritmo a la razón de monomios, tenemos un valor que está en el rango [-∞, ∞]:
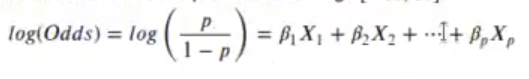
La función de coste de la razón de momios o razón de odds que vamos a tratar de minimizar será:
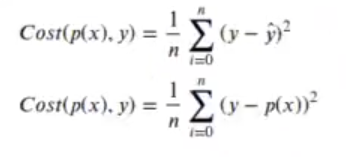
Que transformamos y optimizamos en:

Aquí no miramos el error cuadrático medio, como lo hacíamos en otros ejercicios, sino que únicamente se optimiza hasta quedar en la fórmula de la imagen anterior.
Cuando queremos minimizar la función de coste, que es el error cuadrático medio y sigue un tipo distintivo de distribución, el resultado que obtenemos es la misma función de coste, pero transformada.
In [5] : summary (radar.train)
summary (radar.test)| distancia | potencia | tipo | tipo.n |
| Min. : 16.0 | Min. : 0.002959 | ruido : 22 | Min : 0.0000 |
| 1st Qu. : 88.0 | 1st Qu. : 0.064261 | avion : 20 | 1st Qu. : 0.0000 |
| Median : 152.0 | Median : 0.129854 | Median : 0.0000 | |
| Mean : 201.7 | Mean : 0.150611 | Mean : 0.4762 | |
| 3rd Qu. : 340.2 | 3rd Qu. : 0.253519 | 3rd Qu. : 1.0000 | |
| Max. : 485.0 | Max. : 0.315358 | Max : 1.0000 |
| distancia | potencia | tipo | tipo.n |
| Min. : 47.0 | Min. : 0.02761 | ruido : 7 | Min : 0.0000 |
| 1st Qu. : 142.5 | 1st Qu. : 0.07513 | avion : 1 | 1st Qu. : 0.0000 |
| Median : 259.0 | Median : 0.16085 | | Median : 1.0000 |
| Mean : 261.0 | Mean : 0.15101 | | Mean : 0.6111 |
| 3rd Qu. : 384.0 | 3rd Qu. : 0.19994 | | 3rd Qu. : 1.0000 |
| Max. : 453.0 | Max. : 0.31463 | | Max : 1.0000 |
Vamos a ejecutar el modelo de razón de momios o razón de odds:
In [6] : model <- glm (data = radar.train, formula = tipo ~ distancia + potencia, family = binomial (link = "logit"))
betalg <- model$coefficients
ggplot (radar.train, aes (x = distancia, y = potencia, color = tipo)) + geom_point (size = 3) + geom_abline (intercept = (0.5 -beta [1]) / beta [3], slope = beta [2] / beta[3], color = "red") + geom_abline (intercept = betalg [1] / betalg [3], slope = -betalg [2] / betalg [3], color = "blue")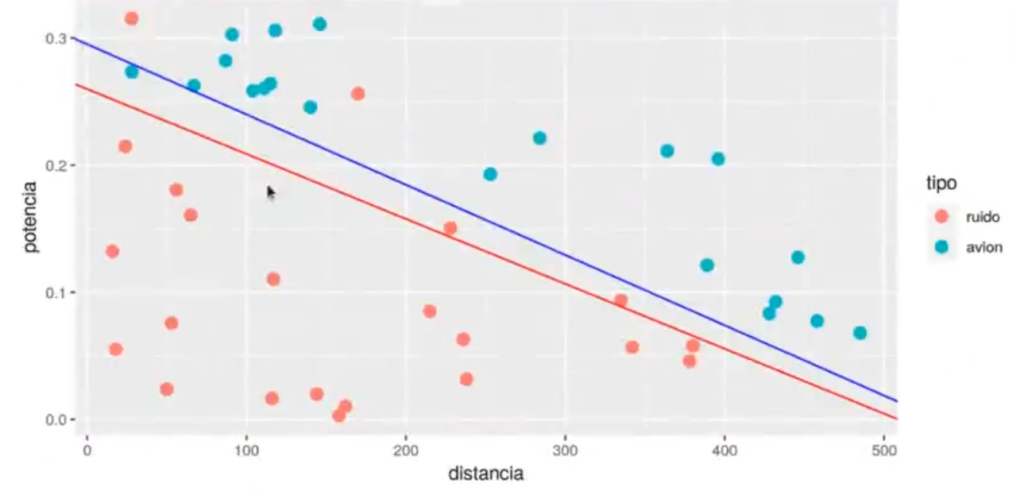
En este caso, hemos hecho la comparación de cómo saldría si hacíamos un modelo con regresión lineal y uno con regresión logística. El modelo de regresión logística sale un poco mejor.
El modelo de logística es el umbral que separa el decir sí (puntos azules) del decir no (puntos rosas). La línea roja corresponde a la regresión lineal y la línea azul hace referencia a la regresión logística.
La salida del modelo es log (odds) de la razón de odds:
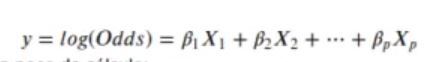
Si queremos la probabilidad, tenemos que aplicar un poco de cálculo:
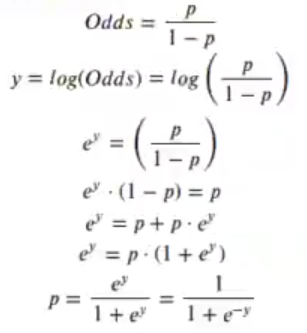
Cuando hacemos un predict, el resultado es el log de las odds o de la razón de momios (señalado con el recuadro naranja):
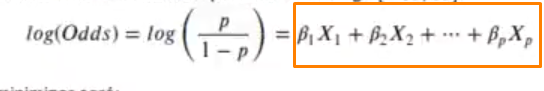
Así, los valores van a ir entre –∞ – ∞, siendo 0 el punto donde las probabilidades son iguales.
In [7] : out <- radar.test
out ["y"] <- predict (model, radar.test)
ggplot (out, aes (x = y, color = tipo)) + geom_histogram (aes (fill = tipo)) + xlab ("odds")‘stat_bin()’ using ‘bins = 30’. Pick better value with ‘binwidth’.

Si no queremos ver este histograma, tenemos varias opciones. Una de ellas es hacer la transformación a mano:
In [15] : out <- radar.test
out ["y"] <- predict (model, radar.test)
#out ["probs"] < exp (out ["y"]) / (1 + exp (out ["y"]))
out ("probs"] <- 1 / (1 + exp(- out ["y"]))
ggplot (out.aes (x = probs.color = tipo)) + geom_density ()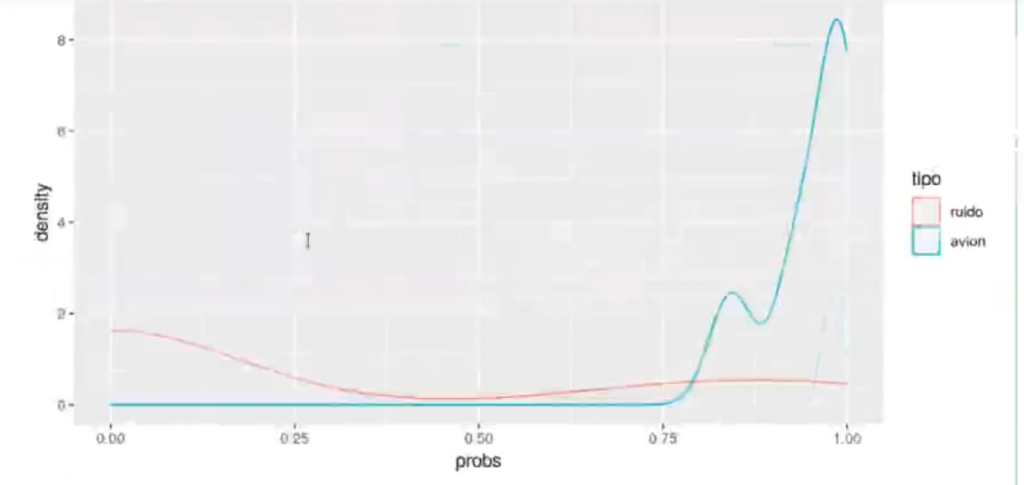
Y otra opción es usar el predict:
In [13] : out ["probs"] <- predict (model, radar.test, type = "response")
ggplot (out, aes (x = probs, color = tipo)) + geom_density ()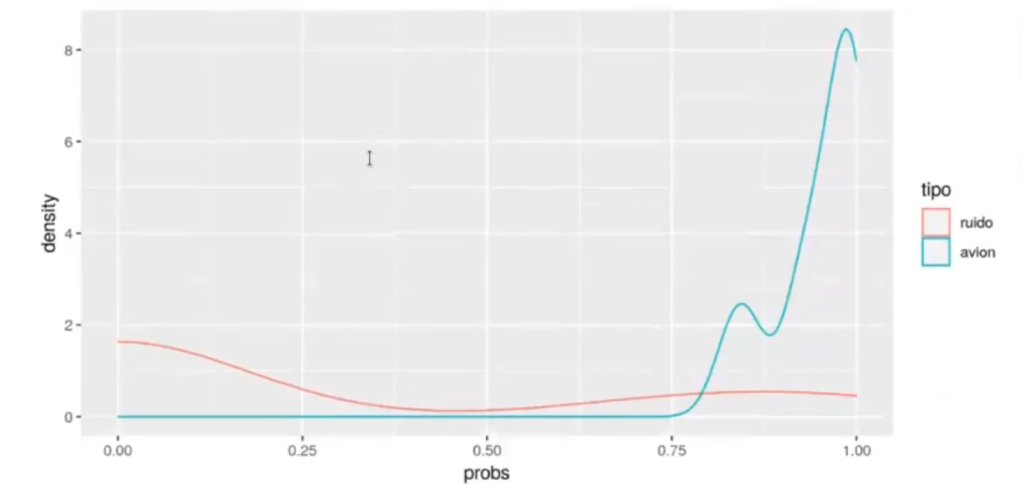
Este ejercicio de la razón de momios se puede evaluar con una matriz de confusión.
Si quieres seguir aprendiendo y entender cómo funciona la matriz de confusión y cómo podemos evaluar la razón de momios a través de ella, te invitamos a inscribirte en nuestro Bootcamp Big Data, con el que, en pocos meses, aprenderás todo lo necesario para incursionar en el gran mundo del Gig Data. ¡Anímate a cambiar tu vida y solicita más información!











