La regresión logística es un proceso de modelado para calcular la probabilidad de un resultado discreto dada una variable de entrada. Se utiliza mucho cuando la variable dependiente (objetivo) es también una variable categórica.
Esta es un método de análisis útil para problemas de clasificación, en los que intenta determinar si una nueva muestra encaja mejor con una categoría.
Tipos de regresión logística
Existen dos tipos de regresión logística:
- La regresión logística binaria, que toma solamente valores como verdadero/falso. Los valores de esta regresión oscilan estrictamente entre 0 y 1. Ambas categorías pueden ser prácticamente cualquier cosa, por ejemplo «compró/no compró el coche», «sacó/no sacó el perro a pasear», etc.
- La regresión logística multinomial, que puede modelar un conjunto de variables en donde hay más de dos posibles resultados discretos.
Ejercicio de regresión logística
En lugar de realizar una predicción de un valor, queremos hacer un clasificador.
Si lo que tenemos son dos grupos y queremos realizar una clasificación, tenemos que realizar ciertas modificaciones a la regresión lineal.
La fórmula de la regresión lineal es:
Ŷ = ß₁X₁ + B²X² + ··· + BpXp = Σ Bk Xk
Podemos tratar de asignar una probabilidad, pero hay un problema, porque esta regresión va entre 0 y 1.
Por ejemplo: trabajamos en un RADAR y queremos saber si hemos detectado un avión o es solo ruido.
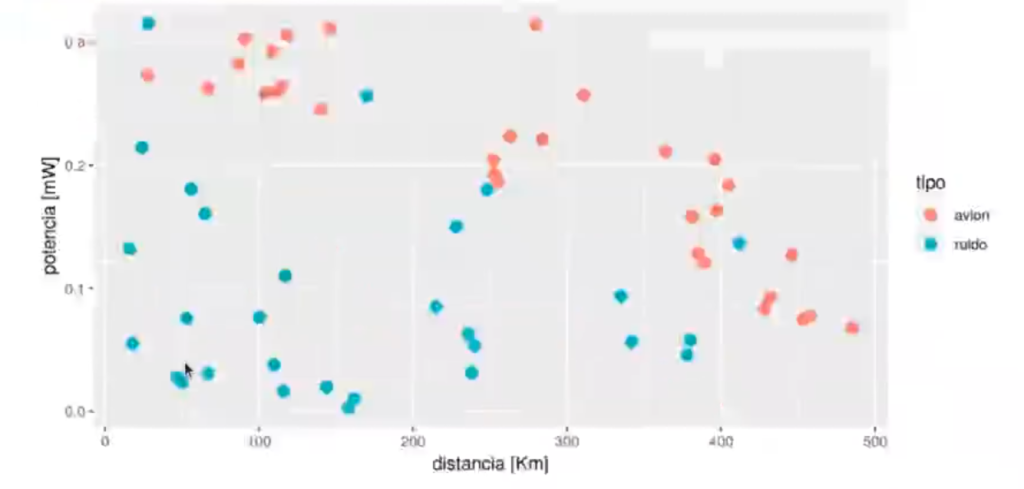
In [1] : options (repr.plot.height = 4, repr.plot.width = 8, repr.plot.res = 300)
library (ggplot2)
radar <- read.csv ("data/radar-lite.csv", stringsAsFactors = T)
summary (radar)
ggplot (radar, aes (x = distancia, y = potencia, color = tipo)) + geom_point (size = 3) + ylab ("potencia [mW]") + xlab ("distancia [Km]")| distancia | potencia | tipo |
| Min. : 16.0 | Min. : 0.002959 | avion : 31 |
| 1st Qu. : 103.0 | 1st Qu. : 0.066766 | ruido : 29 |
| Median : 221.5 | Median : 0.143595 | |
| Mean : 219.8 | Mean : 0.150970 | |
| 3rd Qu. : 367.5 | 3rd Qu. : 0.229278 | |
| Max. : 485.0 | Max. : 0.315358 |
In [2] : radar$tipo <- relevel (radar$tipo, ref = 'ruido')
summary (radar)| distancia | potencia | tipo |
| Min. : 16.0 | Min. : 0.002959 | avion : 29 |
| 1st Qu. : 103.0 | 1st Qu. : 0.066766 | ruido : 31 |
| Median : 221.5 | Median : 0.143595 | |
| Mean : 219.8 | Mean : 0.150970 | |
| 3rd Qu. : 367.5 | 3rd Qu. : 0.229278 | |
| Max. : 485.0 | Max. : 0.315358 |
Podemos hacer una clasificación con un modelo lineal donde creamos una nueva columna tipo.n y le asignamos:
- avion = 1
- ruido = 0
Utilizamos un modelo lineal tal que:
tipo.n = B0 +B1 – distancia + B2 – potencia
Entonces:
- Si tipo.n >= 0.5 es un avión.
- Si tipo.n < 0.5 es ruido.
La recta que marcará el umbral sería:

In [3] : set.seed (1)
set.seed (2)
radar$tipo.n [radar$tipo == "avion"] <- 1
radar$tipo.n [radar$tipo == "ruido"] <- 0
itrain <- sample (l:nrow (radar), round (nrow (radar) * 0.7))
radar.train <- radar [itrain , ]
radar.test <- radar [ - itrain , ]
modellm <- lm (data = radar.train.formula = tipo.n ~ distancia + potencia)
beta <- modellm$coefficients
ggplot (radar.train, aes (x = distancia, y = potencia, color = tipo)) + geom_point (size = 3) + geom_abline (intercept = (0.5 - beta [1]) / beta [3], slope = -beta [2] / beta [3], color = "red")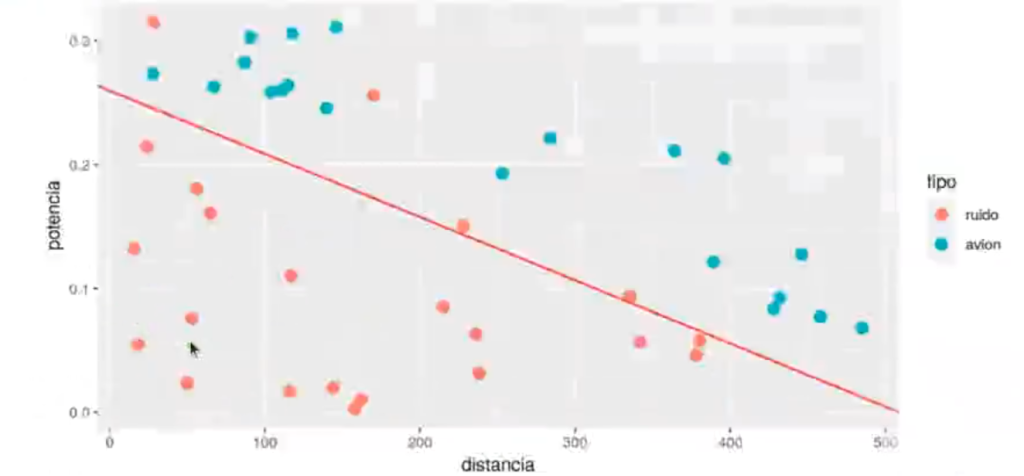
Pero esto no es del todo correcto, porque los datos no siguen una distribución gaussiana, sino una distribución binomial con dos posibles valores: 0 o 1.
La distribución binomial es una generalización de la distribución de Bernoulli para n sucesos independientes, cada uno de los cuales tiene dos posibles resultados: Sí/No con probabilidad p.
Por ejemplo, si tiramos al aire 3 monedas y miramos cuál es la probabilidad de que 2 salgan cara.
Variables que definen la distribución:
- p – probabilidad de éxito de un caso individual.
- n – número de eventos totales que se desean medir.
- k – número de eventos que ha salido SÍ.
Estimadores media (p) y varianza (o2)
u = n . p
o2 = n . p . (1 – p)
Si tenemos n sucesos independientes que siguen una distribución de Bernoulli, ¿cuál es la probabilidad de que l sucesos sean positivos? Si sabemos que la probabilidad de un suceso (k = l) que sigue una distribución de Bernoulli viene dada por la función de distribución:
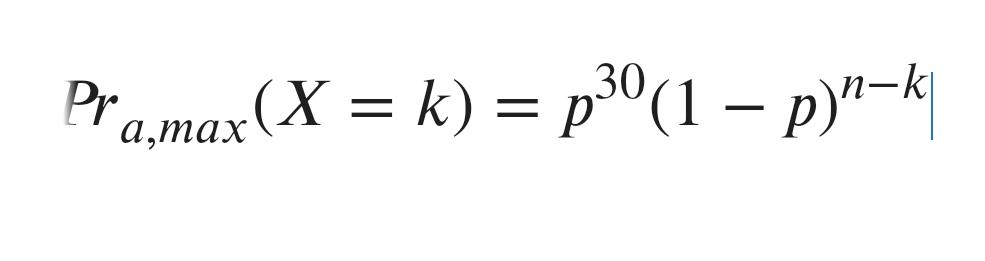
λ E l 0, 1 l
Al tener λ sucesos donde λ E (0, 1, 2…. n), la función será la de Bernoulli multiplicada por el coeficiente binomial que acabamos de ver:
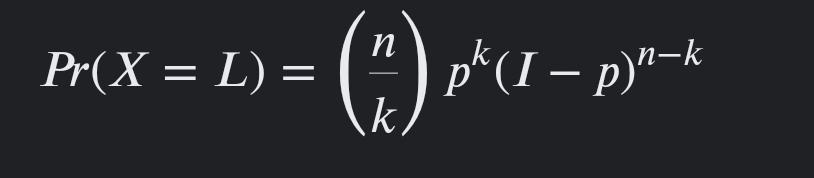
La función acumulativa será:
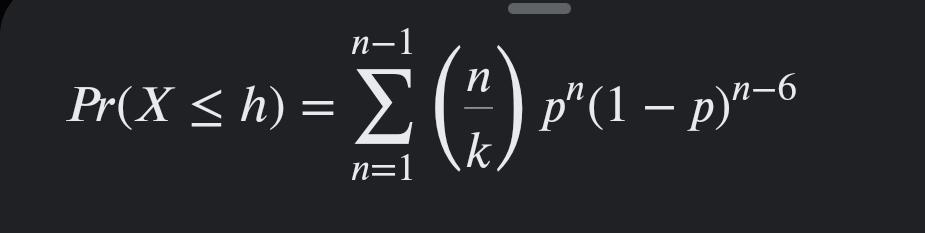
¿Qué sigue?
Ahora que sabemos qué es la regresión logística y cómo funciona el modelo de regresión logística, podemos dar el siguiente paso en la escala del minado de datos. Para poder guiarte mejor, Keepcoding tiene para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en donde aprenderás en muy pocos meses todo lo necesario para incursionar en un mercado laboral lleno de oportunidades de empleo. ¡Solicita ahora más información y apúntate para destacar en el sector IT!











