Una derivada es el resultado de un límite y representa la pendiente de la recta tangente al punto donde se ubica x.
Representación de una derivada
La derivada de una función es su pendiente:
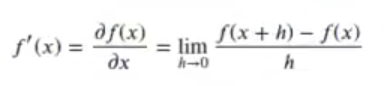
En nuestra función f(x) = x2 + 3, la derivada sería:
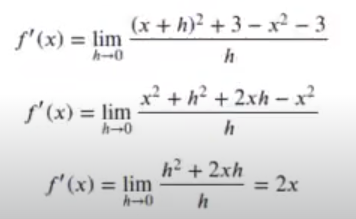
In [25]: # ¿Cómo de pequeño tiene que ser h?
x <- 5
for (h in c(1,0.5,0.1,0.01, 1e-3,le-4,1e-5)){
print((myfunc(x+h)-my func(x))/h)
}
[1] 11
[1] 10.5
[1] 10.1
[1] 10.01
[1] 10.001
[1] 10.0001
[1] 10.00001Podemos pintar la derivada junto con la función.
La derivada es f1(x) = 2x. Lo que hacemos es pintar una recta y= a.x+b. Sabemos que la pendiente es f1(x) = a = 2x. Lo centramos en f(x), así que b= f(x) = 2x, y dibujamos la recta desde [x-delta.x+delta] para:
- x= -7 f1(x)=-14 y f(x)=52
- x= 0 f1(x) =0 y f(x)=3
- x= 5 f1(x)=5 y f(x)=28
Imaginemos una derivada como una montaña. Estás encima de esa montaña y quieres saber hacia dónde va esa pendiente. Das un paso y, si es cuesta arriba, sabrás que la pendiente va hacia arriba; si es cuesta abajo, va hacia abajo.
Es lo mismo que estamos haciendo con la función.
Desglosemos: estás en la función f (x), das un pequeño paso hacia adelante y le sumas h; ahora tienes f(x+h) y compruebas con el valor que tenías antes ahora sería f(x+h)-f(x). En función de cómo de grande o pequeño hayas dado ese paso, el resultado va a ser distinto.
Matemáticamente, se define la derivada como el paso más pequeño que puedes dar, dividido entre ese ancho de zancada que has dado, con la condición de que debes intentar dar esa zancada lo más corta posible.
Entonces, la fórmula quedaría:
f(x+h)-f(x)
—————–
h
Cuanto más pequeño sea h, mejor, porque permite calcular con mayor precisión la derivada.
Sabemos que el Big Data tiene muchísimas vertientes y, por tanto, hay infinidad de temas sobre los cuales puedes aprender. En Keepcoding tienes la posibilidad de aprender con los mejores profesionales, que te guiarán a través de la teoría y la práctica que te permitirán convertirte en un gran profesional del sector IT. Échale un vistazo al temario del Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp y descubre esta formación íntegra e intensiva. ¡No dudes en pedir más información y da el paso que impulsará tu carrera!











