La habilidad de obtener un resultado en datos no observados se llama generalización estadística. El objetivo en la generalización estadística es encontrar el modelo que mejor encaje con los datos observados.
En data mining, queremos un modelo para hacer predicciones; eso significa que necesitamos un modelo que funcione lo mejor posible con datos que no hemos observado nunca.
Es por ello que los datos se dividen en, como mínimo, dos grupos.
- Datos de entrenamiento: los datos con los que entrenaremos nuestro modelo.
- Datos de test: los datos con los que comprobaremos la calidad de nuestro modelo. Son datos que el modelo no ha visto nunca
Un ejemplo de generalización estadística
Supongamos que tenemos los siguientes datos:
In [39]: Library (ggplot2)
x <- c (-1.1, -1.05, 0.99, 0.95, -0.5, -0.55. 0, 0.1, 0.7, 0.71, 0.9, 0.91, 1.5, 1.85, 1.95, 1.99, 2, 2.1, 3, 3.1, -0.20, -0.04, 1.21, 1.59)
y <- c (17.462034, 17.543560, 17.044042, 13.444434, 9.866625, 10.191937, 9.425260, 9.998468, 13.910648, 13.645024, 15.083907)
data.df <- data.frame(x, y)
ggplot (data.df,aes (x = y, y = y)) +geom _point() + theme__linedraw()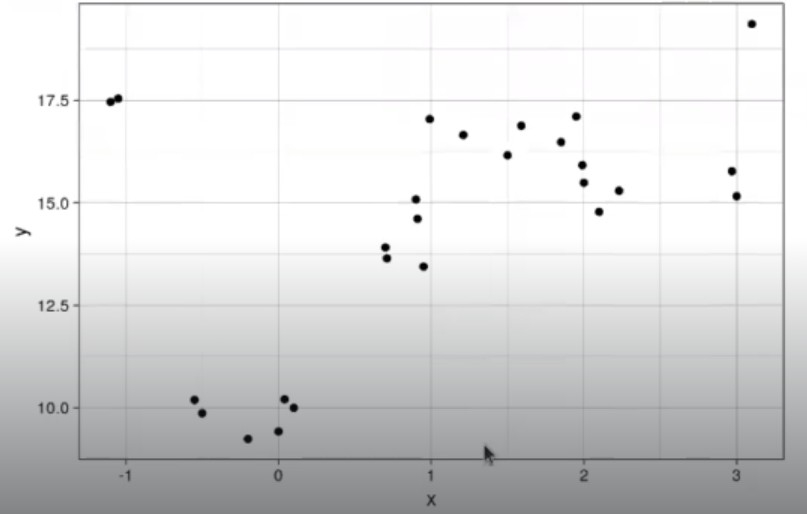
Queremos hacer un modelo que, dado un valor de X, nos dé el valor más cercano a Y. Podemos probar con modelos más o menos complejos:
In [ ]: model <- Im (y-poly (x, 4), data = data.df)
new.data.df <- data.frame (x = c (data.df$x, seq (-1,3, length.out-100)), y= NA, yp = NA)
new.data.dfsyp <- predict (model, new.data.df)
data.df$yp <- predict (model, data.df)
new.data.df <- rbind (new.data.df, data,df)
ggplot (new.data.df,aes (x = x, y = y)) + geom_point (na.rm = TRUE) + geom_line (aes (y=yp, color = "blue") + theme_linedraw()
caret:: postResample (pred = data.df$yp, obs= data.df$y)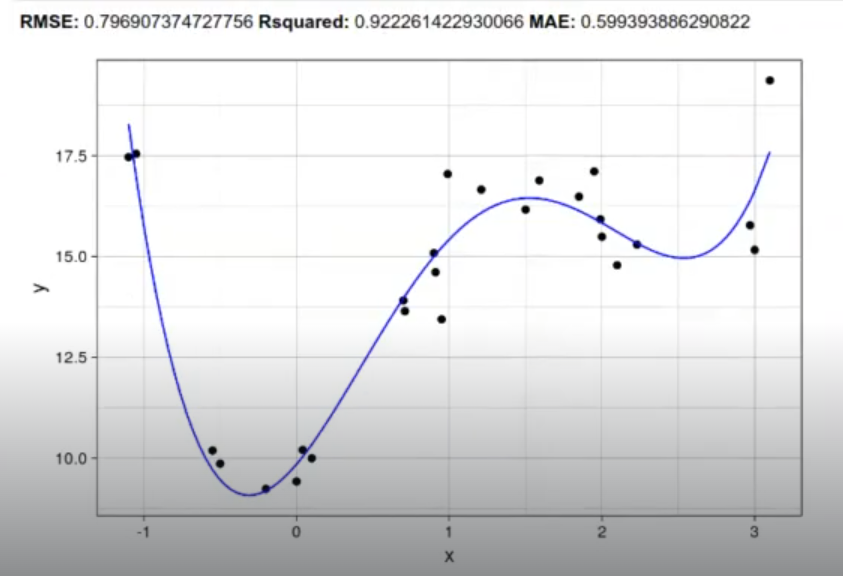
¿Cuál de todos los modelos es el mejor? Recuerda que buscamos generalización estadística, por lo que queremos que el modelo se comporte lo mejor posible con datos que no ha visto. Por ello, dividimos nuestros datos entre test y training. Una buena práctica consiste en usar un 70%-80% para entrenamiento y el resto para test. En este caso, podemos, por ejemplo, coger 20 muestras para entrenamiento y el resto para test.
El siguiente paso para probar la generalización estadística sería generar los training y los testing. Si quieres seguir aprendiendo sobre este proceso y mucho más para forjar tu futuro como especialista en el sector IT, nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp es tu mejor opción.
En pocos meses, con la guía de nuestros profesores expertos, dominarás todo lo relacionado con el mundo del Big data y podrás entrar en un mercado laboral lleno de oportunidades. ¡Anímate a solicitar más datos!











