¿Qué es una matriz invertible?

¿Sabes qué es una matriz invertible y cómo calcularla en Python?

Como puedes leer en el artículo sobre el menor complementario, una matriz invertible es aquella que viene dada por la desigualdad |A| ≠ 0 (que el determinante sea diferente a cero). Es decir, en la ecuación A_ij = (-1)^i + j. a_ij, si i + j es par, coincide el adjunto con el menor complementario, mientras que si i + j es impar, tendrán valores opuestos.

En caso de que el determinante sea igual a 0, no se podrá calcular la inversa de esa matriz y esta se denominará matriz singular.

Calcular una matriz invertible

Veamos un ejercicio en Python sobre cómo calcular una matriz invertible, así podemos entender un poco mejor este concepto.

Determinemos si la siguiente matriz es invertible:

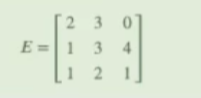
Lo primero que haremos es definir la matriz con cada una de las filas y columnas. Lo que haremos luego es calcular la inversa. Aplicando np.linalg.inv, podemos resolver este punto. Posteriormente, solo nos queda imprimir la matriz:

#matriz invertible
E = np.array ([[2,   3,   0],
                         [1,   3,   4],
                         [1,   2,   1]])

inv_E = np.linalg.inv (E)
inv_E

array (

[[5., 3., -12.],

[-3., -2., 8.],

[1., 1., -3.]])

Ya vemos cómo podemos calcular la inversa usando esta función. Y si calculamos el determinante de esta matriz, vemos que es distinto a cero.

#matriz invertible
np.linalg.det (E)

-0.9999999999999996

¿Qué sucede para la siguiente matriz?

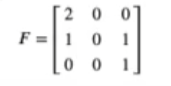
#matriz invertible
F = np.array ([[2,   0,   0],
                         [1,   0,   1],
                         [0,   0,   1]])

inv_F = np.linalg.inv (F)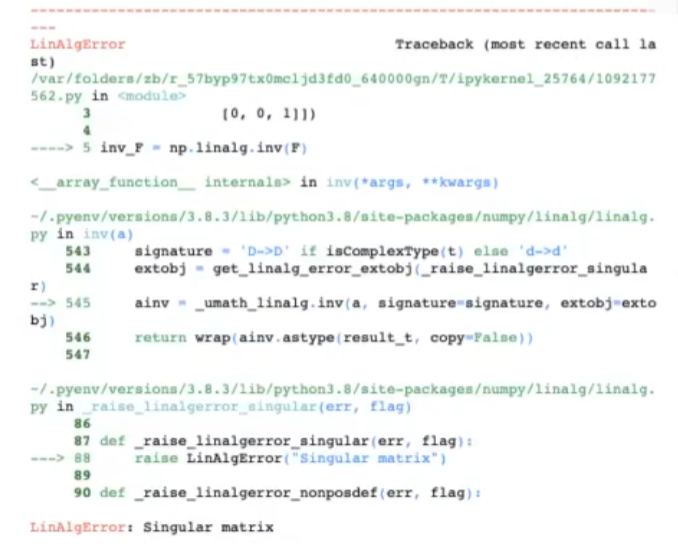

Como habrás notado, con este último ejemplo de matriz que hemos puesto se da el caso contrario, donde la matriz no es invertible.

Al igual que con el primer ejemplo, definimos la matriz e intentamos calcular la inversa. No obstante, cuando Numpy intenta calcular la inversa de una matriz y no puede, porque esta es singular, nos manda un mensaje de error diciendo que es una «Singular matrix», en lugar de devolver un resultado.

Podemos comprobar esto simplemente calculando el determinante de esta función:

#matriz invertible
det_F = np.linalg.det (F)
det_F

0.0

Como su determinante es 0, no podemos calcular la inversa de la segunda matriz y, por tanto, la matriz F en este caso es una matriz singular.

Si quieres acceder a una de las disciplinas más demandadas y mejor pagadas dentro del mercado laboral, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación íntegra en la que podrás obtener, en pocos meses, todos los conocimientos teóricos y prácticos que te ayudarán a lograr tu trabajo soñado. ¡Entra ya para solicitar información y cambia tu futuro con la guía de los mejores profesionales!