¿Qué es la Ley de Zipf?

¿Sabes qué es la Ley de Zipf y en qué consiste? Esta ley fue formulada en la década de 1940 por el lingüista George Kingsley Zipf y establece que, dada una lengua, la frecuencia de aparición de las distintas palabras de su vocabulario sigue una distribución que puede aproximarse por:

P_n ~ 1 / n^a

Veamos qué relación tiene esto con el machine learning y, más específicamente, con el NLP o Natural Language Processing.

¿En qué consiste la Ley de Zipf?

La Ley de Zipf es una ley empírica que sigue una distribución estándar, es decir, siempre, pongamos las palabras que pongamos, van a seguir la misma distribución. Si cogemos un vocabulario cualquiera, las palabras, de las más frecuentes a las menos frecuentes, tienen una distribución que va a visualizarse del mismo modo. Vamos a ver un gráfico log – log con el ranking y la asiduidad de los 10 millones de palabras más frecuentes para distintos idiomas:

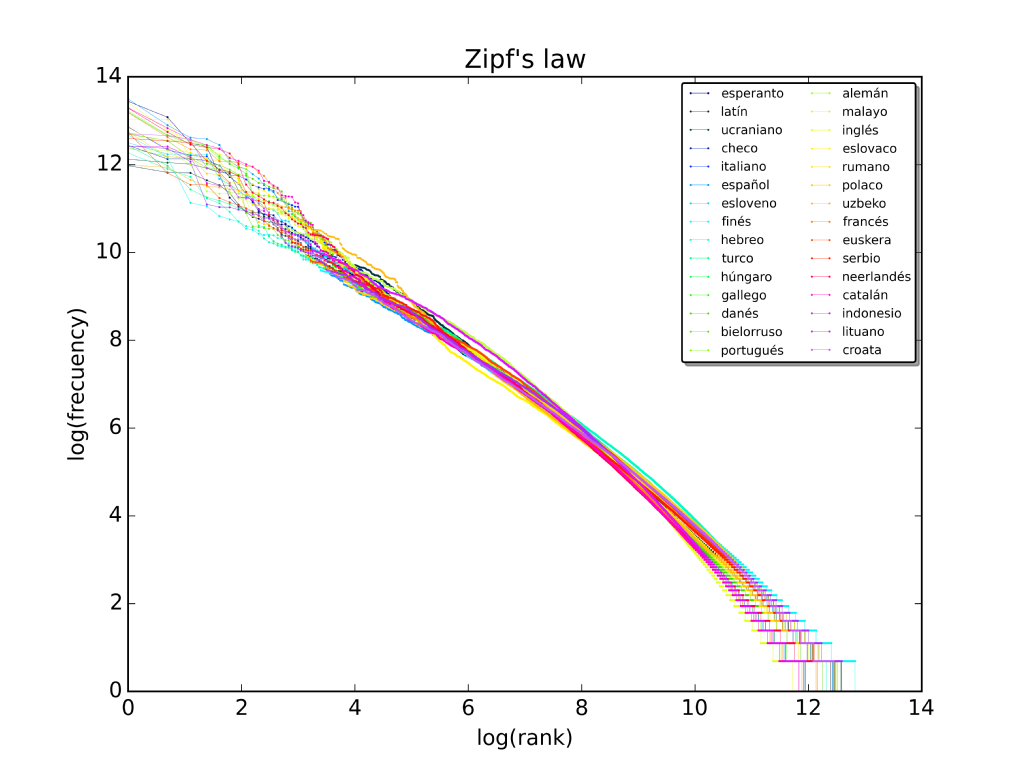
En el ámbito del machine learning y, para ser más específicos, el NLP o Natural Language Processing, la ley de zipf español es una distribución de probabilidad discreta que nos indica la probabilidad de encontrar una palabra en un corpus dado. La entrada es el rango de una palabra, hablando en términos de frecuencia, por lo que se puede usar esta distribución para realizar preguntas como: ¿en un corpus de n-mil palabras, cuál es la palabra más recurrente?, ¿existe alguna probabilidad de encontrar la quinta palabra más común en un corpus de 250.000 palabras o n-mil palabras?

Debido a que los modelos de lenguaje neuronal representan cada palabra en un corpus usando un vector, estos modelos tienden a funcionar mejor con palabras comunes que con palabras que sean poco usadas o raras. Esto es debido a que las palabras poco usadas ocuparán el mismo espacio vectorial que las palabras comunes, aun teniendo un número mucho menor de datos de entrenamiento.Todo esto sucede debido a la Ley de Zipf, donde evaluamos la recurrencia de las palabras.

Veamos un ejemplo

Ahora, vamos a recoger algunas palabras de un texto que ya hemos trabajado en artículos previos. Pintaremos con matplotlib. También usaremos las mismas funciones que hemos utilizado antes y se lo pasamos al método:

#Ley de Zipf
import matplotlib.pyplot as plt
from nltk.probability import FreqDist

#Ley de Zipf
fd = FreqDist (words)

#Ley de Zipf
fd

Tenemos, por tanto, las palabras con sus respectivas frecuencias.

Ahora lo que haremos es ordenar las palabras y las vamos a meter en un diccionario, donde vamos a tener ordenados por palabra y frecuencia cada uno de los ítems:

#Ley de Zipf
fd = {k: v for k, v in sorted (fd.items (), key = lambda item: item [1], reverse = True)}

Ahora vamos a generar dos listas, una para hacer el ranking y otra para alojar las frecuencias, de cara a poder visualizar la ley que estamos trabajando, que es la ley de zipf , y ver cómo saldría el gráfico que planeamos dibujar para el vocabulario del texto que hemos cargado previamente.

De modo que generamos los rankings y las frecuencias:

#Ley de Zipf
ranks = list ()
freqs = list ()

for rank, word in enumerate (fd):
      ranks.append (rank + 1)
      freqs.append (fd [word])

Y lo visualizamos:

#Ley de Zipf
plt.loglog (ranks, freqs)
plt.xlabel ('Rank')
plt.ylabel ('Freq')
plt.title ('Log - Log rank - freq chart')
plt.show ()

Vemos que, de manera empírica, sigue esta distribución con las palabras que más se repiten:

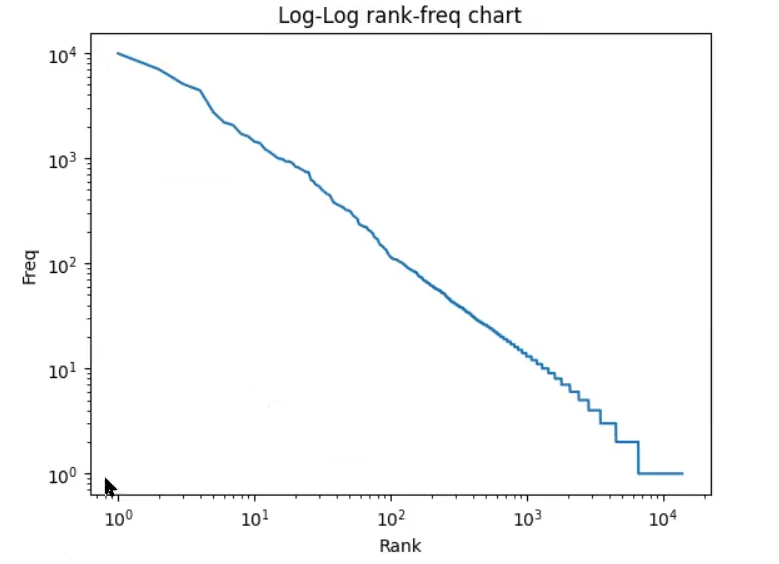
Como se muestra, las más repetidas son las que tienen mayor frecuencia, y las que menos se repiten, por tanto, tienen menor frecuencia. Esto se realiza para cualquier corpus que tengamos en cualquier idioma.

Ahora que hemos visto cómo funciona la Ley de Zipf y un ejemplo sobre esta, es el momento de seguir aprendiendo. Para acceder a las opciones laborales del Big Data, una de las áreas del mundo IT mejor pagadas y con mayor demanda, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Con esta formación intensiva e íntegra adquirirás todos los conocimientos (a nivel teórico y práctico) necesarios para conseguir el trabajo de tus sueños en poco tiempo. ¡No sigas esperando para impulsar tu carrera y pide ahora mismo más información!