Cuando analizamos datos, rara vez tenemos acceso a toda la población. En su lugar, trabajamos con muestras y, a partir de ellas, hacemos inferencias. Aquí es donde entran en juego los intervalos de confianza, una herramienta estadística fundamental para estimar parámetros desconocidos con un margen de seguridad.
En este artículo, exploraremos qué son los intervalos de confianza, cómo se interpretan, cómo se calculan y en qué contextos se utilizan, con ejemplos claros y aplicaciones en el mundo real.
¿Qué son los intervalos de confianza?
Los intervalos de confianza (IC) son un rango de valores que probablemente contenga el verdadero valor de un parámetro poblacional (como una media o una proporción) con un nivel de confianza determinado.
Por ejemplo, si realizamos una encuesta para conocer el salario medio de los desarrolladores en España y obtenemos un IC del 95% de 45.000 a 50.000 euros, esto significa que estamos un 95% seguros de que el salario medio real de todos los desarrolladores se encuentra dentro de ese rango.
¿Cómo se interpretan los intervalos de confianza?
Un error común es pensar que un intervalo de confianza del 95% significa que hay un 95% de probabilidad de que el valor real esté en el intervalo. En realidad, lo que significa es que si repitiéramos el mismo experimento muchas veces, en el 95% de los casos el intervalo incluiría el valor real.
Otra interpretación clave es que un intervalo más amplio indica más incertidumbre, mientras que un intervalo más estrecho indica una estimación más precisa.
¿Cómo se calcula un intervalo de confianza?
El cálculo de un IC depende del tipo de parámetro que queremos estimar y de la distribución de los datos. La fórmula general para calcular un intervalo de confianza para la media poblacional cuando la desviación estándar es desconocida es:

Donde:
- x̄ es la media muestral
- Z es el valor crítico de la distribución normal para el nivel de confianza deseado (por ejemplo, 1.96 para un 95% de confianza)
- σ es la desviación estándar de la población
- n es el tamaño de la muestra
Cuando la muestra es pequeña (n < 30) y la desviación estándar de la población es desconocida, se usa la distribución t de Student en lugar de la distribución normal.
Veamos un ejemplo
Supongamos que realizamos un estudio sobre el número de ciberataques en empresas tecnológicas. A partir de una muestra de 100 empresas, obtenemos:
- Media muestral: 75 ataques al año
- Desviación estándar: 20 ataques
- Nivel de confianza: 95%
Aplicando la fórmula:
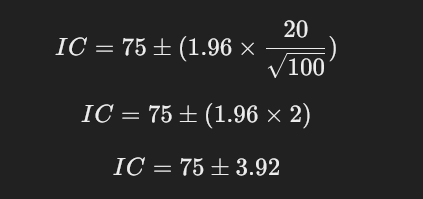
El intervalo de confianza sería (71.08, 78.92), lo que significa que, con un 95% de confianza, el número real de ataques en empresas tecnológicas está dentro de ese rango.
Factores que afectan el intervalo de confianza
El ancho de un intervalo de confianza está influenciado por varios factores:
- Tamaño de la muestra: Cuanto mayor sea la muestra, más estrecho será el intervalo.
- Variabilidad de los datos: Si los datos son más dispersos, el intervalo será más amplio.
- Nivel de confianza: A mayor confianza (por ejemplo, 99% en lugar de 95%), el intervalo será más grande.
Errores comunes al interpretar los intervalos de confianza
- Confundir un intervalo de confianza con un rango de valores posibles: El intervalo de confianza no garantiza que el valor real esté dentro de él en una única muestra.
- No considerar el tamaño de la muestra: Un intervalo estrecho con pocos datos puede ser engañoso.
- Asumir que un intervalo más amplio es siempre mejor: Un intervalo demasiado grande puede ser poco útil para la toma de decisiones.
Los intervalos de confianza son herramientas esenciales en la estadística, ya que nos permiten estimar con un margen de seguridad qué tan cercanos estamos al valor real de una población. Su correcta interpretación es clave para tomar decisiones informadas en sectores como la ciencia de datos, la salud y la ciberseguridad. Si quieres aprender a aplicar técnicas estadísticas avanzadas para el análisis de datos y la inteligencia artificial, el Bootcamp en Big Data y Machine Learning de KeepCoding te brindará el conocimiento práctico y la orientación experta que necesitas para destacar en la industria tecnológica.











