Las matemáticas actuariales son una rama especializada de las matemáticas aplicadas que se utilizan principalmente en la gestión de riesgos financieros en sectores como los seguros, las pensiones y las inversiones. Gracias a ellas, los actuarios pueden modelar escenarios futuros, calcular probabilidades de eventos y diseñar productos financieros que minimicen riesgos e incrementen rentabilidad.
En este artículo, exploraremos qué son las matemáticas actuariales, sus principales aplicaciones y ejercicios prácticos para comprender su funcionamiento.
¿Qué son las matemáticas actuariales?
Las matemáticas actuariales combinan principios de estadística, probabilidad y análisis financiero para evaluar riesgos e incertidumbres en escenarios económicos. Se basan en modelos matemáticos para prever eventos como la longevidad de una población, la rentabilidad de un fondo de inversión o la posibilidad de siniestros en un seguro.
Esta disciplina tiene aplicaciones directas en sectores como:
- Seguros de vida y salud: Cálculo de primas, reservas y probabilidades de siniestros.
- Pensiones y jubilaciones: Modelado de esperanza de vida y sostenibilidad de fondos de retiro.
- Inversiones y finanzas: Análisis de carteras de inversión y estrategias de cobertura.
Fundamentos matemáticos de la ciencia actuarial
Las matemáticas actuariales se apoyan en diversas ramas de la matemática y la estadística. Algunas de las herramientas más utilizadas incluyen:
- Probabilidades y distribuciones estadísticas: Los actuarios trabajan con modelos probabilísticos para evaluar incertidumbres. Por ejemplo, la distribución de Poisson se usa para estimar la frecuencia de eventos en un período de tiempo determinado, como el número de siniestros en una aseguradora.
- Matemática financiera: Los cálculos actuariales dependen de fórmulas de valor presente y valor futuro, especialmente en la valoración de rentas y pensiones. Una fórmula clave es la del valor actual de una renta vitalicia, que permite calcular cuánto se necesita invertir hoy para recibir pagos periódicos en el futuro.
Ejemplo: Si deseas recibir una renta mensual de $1,000 durante 20 años con una tasa de interés del 5% anual, ¿cuánto debes invertir hoy?
La respuesta se obtiene con la fórmula de valor actual de una anualidad:
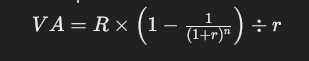
Donde:
- VA es el valor actual
- R es la renta periódica ($1,000)
- r es la tasa de interés (0.05 anual)
- n es el número de periodos (240 meses)
- Modelos de Supervivencia: La longevidad de una población influye en seguros y pensiones. Se utilizan tablas de mortalidad, como las creadas por aseguradoras, para estimar la esperanza de vida y calcular primas adecuadas.
Ejemplo práctico: Si una compañía de seguros quiere determinar la probabilidad de que una persona de 60 años viva hasta los 80, debe analizar los datos de la tabla de mortalidad y aplicar la función de supervivencia.
¿Quieres practicar? ¡Aquí te van algunos ejercicios!
Para afianzar los conceptos en matemáticas actuariales, aquí tienes algunos ejercicios básicos:
- Cálculo de primas de seguro
- Una aseguradora ofrece un seguro de vida de $100,000 a un individuo de 35 años. Si la probabilidad de fallecimiento en un año es del 0.2% y la aseguradora busca un margen de ganancia del 10%, ¿cuál debería ser la prima anual?
- Determinación del valor esperado
- Un fondo de pensiones espera pagar $2,000 mensuales a un jubilado durante 25 años. Si la tasa de descuento es del 4% anual, ¿cuál es el valor presente de este compromiso financiero?
- Probabilidad de siniestros
- En una compañía aseguradora, el número de accidentes de tráfico sigue una distribución de Poisson con una media de 5 accidentes por día. ¿Cuál es la probabilidad de que ocurran exactamente 3 accidentes en un día dado?
Las matemáticas actuariales son esenciales para evaluar riesgos y tomar decisiones informadas en sectores como seguros, finanzas y pensiones. Si deseas dominar estas herramientas y aplicarlas en el mundo real, el Bootcamp de Big Data y Machine Learning de KeepCoding te proporcionará el conocimiento necesario para trabajar con modelos predictivos, análisis de datos y algoritmos de machine learning aplicados a la gestión financiera y actuarial.











