Saber qué son las distribuciones en estadística Big Data es uno de los conocimientos que utiliza esta rama del estudio de los macrodatos y su importancia radica en que el análisis exploratorio de datos es el primer paso que todo data scientist tiene que tomar.
De hecho, es conocido que todo buen data scientist tiene que tener una buena base de estadística, puesto que esta te permite saber si ciertas variables tienen relación o no o si varios grupos de datos se pueden considerar diferentes o iguales.
Por esta razón, en este post, te compartimos qué son las distribuciones en estadística Big Data.
Como primer instancia para comprender qué son las distribuciones en estadística Big Data, hay que partir de los principales propósitos de esta última, ya que consiste en entender las variables de la información y la relación entre las variables que se encuentran en ella. La estadística te ayudan a comprender cómo es tu población de los datos. Para ello, esta cuenta con ciertos elementos, como los percentiles, la varianza, los estimadores, la moda, los tests estadísticos, las operaciones, las asignaciones, etc.
En definitiva, la estadística en el Big Data se dedica a analizar los datos de manera minuciosa para, posteriormente, identificar las coincidencias de variables con las que cuenta la información.
¿Qué son las distribuciones en estadística Big Data?
Las distribuciones en estadística Big Data forman parte de las funciones de probabilidad conocidas, es decir, las que aparecen con mayor frecuencia cuando se realiza algún tipo de estudio estadístico. Ahora bien, las distribuciones en estadística Big Data se encuentran en dos grandes grupos: distribuciones continuas y discretas.
Por otra parte, estas distribuciones son propiedades en las que, por ejemplo, supones que f(x) es la función de densidad de la probabilidad de una variable aleatoria x que se encuentra en los datos procesados.
Su integral, es decir, la suma a lo largo de todo el dominio es igual a 1. Esto significa que la suma de probabilidades de todos los posibles valores será 1. Ahora, esto depende del tipo de distribución.
- Para una distribución continua será:
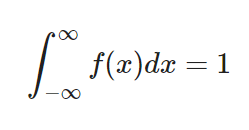
- Para una distribución discreta será:
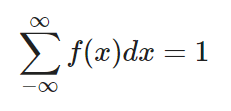
Por otra parte, su integral (la suma), a lo largo de los dos puntos [a, b], da la probabilidad de que la variable aleatoria x caiga en ese rango.
- Para una distribución continua será:
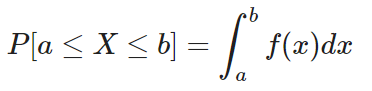
- Para una distribución discreta será:
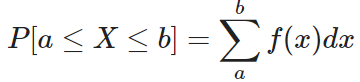
Por ejemplo
Si se elige una persona al azar en España, ¿cuál es la probabilidad de que sea un milenial?
Según la Wikipedia, los milenials podrían comprender los nacidos entre 1980 y 2000, por lo que la operación sería así:
f_poblacion <- poblacion[,c(«Total»,»edad»)]
f_poblacion$nacimiento <- 2019-f_poblacion$edad
# Completar
paste(«La probabilidad de que eligiendo una persona al azar en España sea milenial es «,
f_poblacion_milenial)
Función de distribución acumulativa
Esta función te dice la probabilidad de obtener un valor menor o igual a cierto umbral dado en la variable aleatoria x.
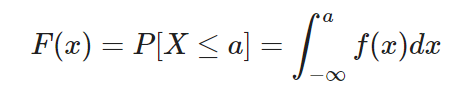
Por ejemplo, si eliges una persona al azar en España, ¿cuál es la probabilidad de que sea menor o igual de 64 años?
# Completar
paste0(«La probabilidad de que eligiendo una persona al azar su edad sea menor o igual a 64 años es «,
round(sum(f_poblacion_subset$Total),3)*100,»%»)
Funciones de probabilidad conocidas
A continuación, te compartimos las funciones de probabilidad que aparecen con mayor frecuencia cuando se realiza algún estudio estadístico.
Todas están relacionadas entre sí como verás a continuación a modo resumen:
- Distribución uniforme: continua. Todos los valores tienen la misma posibilidad.
- Distribución Bernoulli: discreta. Dos posibles soluciones; por ejemplo, una moneda al aire.
- Distribución Binomial: discreta. Generalización de Bernoulli: por ejemplo, tirar varias monedas al aire.
- Distribución Poisson: discreta. Generalización de Binomial cuando hay infinitos eventos de probabilidad muy baja.
- Distribución Exponencial: continua. Tiempo medio entre ocurrencia de eventos de una distribución de Bernoulli.
- Distribución Gaussiana: continua. La distribución más usada, toda combinación de variables aleatorias tiende a una gaussiana.
- Distribución Chi cuadrado: continua. Es el cuadrado de una distribución gaussiana.
Por medio de este post, te has acercado a lo que son las distribuciones en estadística Big Data para un análisis de los datos que logre destacar el valor que representan y sus respectivas relaciones. Ahora bien, este tipo análisis posee una gran variedad de herramientas para llevarse a coba de forma efectiva, por lo que aún falta mucho más por aprender al respecto.
Por este motivo, desde KeepCoding te ofrecemos nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, con el que podrás potenciar tus destrezas en el manejo de los macrodatos y sus múltiples herramientas, lenguajes y sistemas. Aprenderás todo lo necesario en menos de nueve meses de la mano de los mejores profesionales del sector a través de una metodología hands on, centrada tanto en la parte teórica como en la práctica para que le saques el máximo partido a cada módulo. ¡Apúntate ahora y no esperes más para seguir aprendiendo!



