¿Sabes qué son los mínimos cuadrados y cuál es su función? En este post te lo enseñamos.
En otros artículos hemos visto qué es una regresión y cómo se clasifican algunos problemas de machine learning, como en el caso del géiser. ¿Cómo podemos determinar los parámetros w que nos devuelve la recta que mejor se ajusta a los datos? Si recapitulamos un poco, tenemos un conjunto de datos (x1 ; y1)…(xn ; yn) y queremos usar estos datos para determinar w, tal que yi ≈ f (xi, w). Sin embargo, antes debemos tener una objective function para determinar qué valores de w tomamos por buenos. Para ello vamos a emplear los mínimos cuadrados.
Mínimos cuadrados
Los mínimos cuadrados nos ayudan a elegir valores de w que minimizan la suma de los errores al cuadrado.
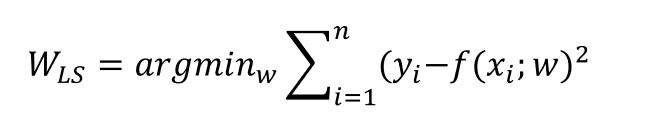
argmin = Minimizar
La anterior es la función de pérdida. Al final hay un cuadrado porque la función tiene que ser convexa. Recordemos que las funciones convexas son funciones con la capacidad de ser fácilmente derivables y, por tanto, fácilmente optimizables.
Vamos, pues, a calcular la distancia vertical del error. Queremos que sea al cuadrado para evitar que la función tenga un pico, lo cual nos facilita el trabajo de calcular la derivada y, del mismo modo, optimizar dicha función.
El objetivo de los mínimos cuadrados L es minimizar la suma de los errores al cuadrado. Si observamos el siguiente plano, la distancia vertical es el error:
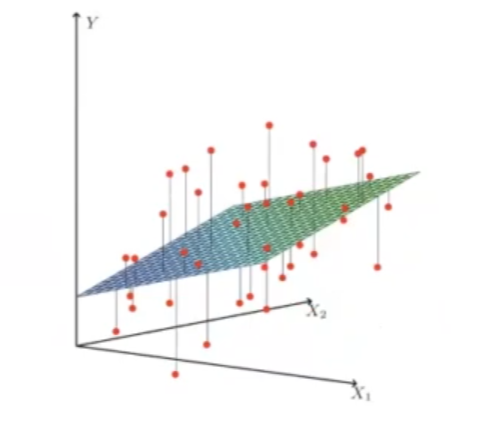
Tenemos los puntos rojos, que son nuestros datos. El plano que vemos es el plano que nos da nuestro modelo. Lo que estamos haciendo simplemente es calcular la distancia que hay entre el punto de nuestros datos, representados con color rojo, y el punto predicho por nuestro modelo, que sería el que corresponde al plano.
Ejemplo de mínimos cuadrados
Aquí hay un ejemplo muy sencillo en el que tenemos como entrada un vector de dos dimensiones con medidas de educación y antigüedad, y como salida tenemos el salario. Queremos predecir los ingresos de una persona en función de su educación y su antigüedad (tenemos como referente la edad o los años que lleve en la empresa).
Tenemos este ejercicio en tres dimensiones. Como estamos trabajando en tres dimensiones, tenemos un plano.
En un eje tenemos el salario, que correspondería a los datos de salida; en los otros dos ejes tenemos los años de educación y la antigüedad, que representan los datos de entrada.
Si eso lo representamos, los puntos rojos indicarían nuestros datos y el plano indicaría el resultado de nuestro modelo.
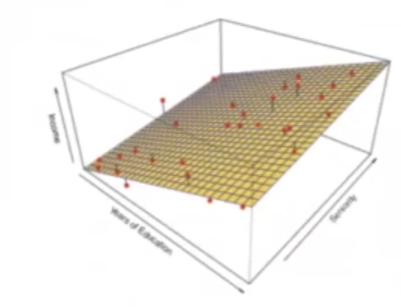
Input: (Educación, Antigüedad) ∈ R2
Output: Salario ∈ R
Model:
salario ≈ w0 + (educación) . w1 + (antigüedad) . w2
Entonces, si nos centráramos simplemente en qué estaría dando nuestro modelo, sería salario, el cual sería aproximadamente igual al parámetro w0, más educación, que es una variable que conocemos por w1, más antigüedad por w2.
Este ejercicio es exactamente igual al ejercicio que hicimos en el artículo del géiser mencionado al principio. Lo único que hemos cambiado es lo que conocemos. En el otro ejercicio queríamos el tiempo de espera y teníamos la duración de la erupción. En este nuevo caso, queremos el salario y tenemos como parámetros la educación y la antigüedad.
¿Quieres seguir avanzando en tu formación profesional?
El Big Data es una de las áreas en las que más trabajos se ofertan. Para poder acceder a este tipo de opciones laborales, unas de las más prolíficas y mejor pagadas, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva e íntegra en la que adquirirás todos los conocimientos teóricos y prácticos que te permitirán obtener el trabajo de tus sueños en pocos meses. Recuerda que en todo momento tendrás el acompañamiento de los mejores profesionales que podrán resolver todas tus inquietudes y te guiarán en el cumplimiento de tus objetivos o metas. ¡No esperes más para impulsar tu carrera y solicita información ahora!











