Los problemas NP-completos representan uno de los mayores desafíos en la teoría de la complejidad computacional. Son problemas que, aunque sus soluciones pueden verificarse en tiempo polinómico, no se conoce un algoritmo eficiente para resolverlos en todos los casos. Esta característica los convierte en el epicentro de un debate que ha marcado la historia de la computación: ¿P es igual a NP?. Comprender estos problemas no solo es crucial para la informática teórica, sino que también tiene aplicaciones prácticas en optimización, criptografía e inteligencia artificial.
¿Qué son los problemas NP-Completos?
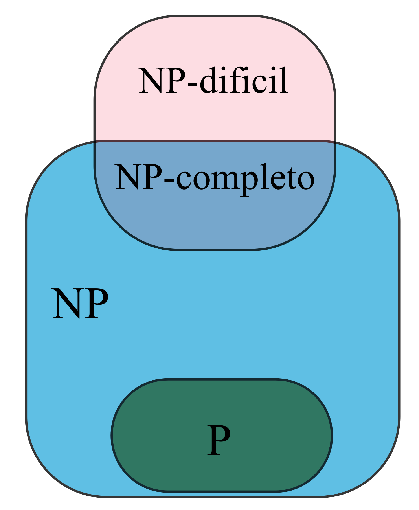
Para entender la categoría de un problema NP completo, es necesario conocer tres clases fundamentales de complejidad computacional:
- P (Polinómico): Problemas que pueden resolverse en tiempo polinómico por un algoritmo determinista. Ejemplo: la suma de dos números.
- NP (No Determinista en Tiempo Polinómico): Problemas cuya solución puede verificarse en tiempo polinómico, aunque no se conozca un método eficiente para resolverlos. Ejemplo: la factorización de números primos.
- NP-Completo: Problemas que son tanto NP-difíciles como pertenecientes a NP, lo que significa que si se encontrara un algoritmo eficiente para resolver uno de ellos, todos los problemas de NP podrían resolverse en tiempo polinómico.
El concepto de NP-completitud fue introducido en 1971 por Stephen Cook en su famoso Teorema de Cook, que demostró que el Problema de la Satisfacibilidad Booleana (SAT) es NP-completo, estableciendo la base para la clasificación de muchos otros problemas dentro de esta categoría.
Tipos y ejemplos de problemas NP-Completos
A lo largo de los años, se ha identificado una gran variedad de problemas NP-completos en diferentes áreas de la informática y las matemáticas. Algunos de los más conocidos incluyen:
- Problema de la Satisfacibilidad Booleana (SAT): Este problema consiste en determinar si existe una asignación de valores de verdad que satisfaga una fórmula booleana dada. Es ampliamente utilizado en verificación de hardware, inteligencia artificial y optimización.
- Problema del Viajante (TSP – Traveling Salesman Problem): Un viajante debe recorrer un conjunto de ciudades exactamente una vez y regresar a su punto de partida, minimizando la distancia total recorrida. Es un problema crucial en logística, planificación de rutas y redes de transporte.
- Problema del Clique: Dado un grafo, se busca encontrar el subconjunto más grande de vértices donde todos están conectados entre sí. Es ampliamente usado en redes sociales y bioinformática para detectar comunidades o patrones en grandes volúmenes de datos.
- Problema de la Mochila (Knapsack Problem): Se trata de seleccionar objetos con diferentes pesos y valores para maximizar el beneficio total sin exceder la capacidad de una mochila. Es clave en finanzas, gestión de recursos y compresión de datos.
Estos son solo algunos ejemplos, pero existen cientos de problemas clasificados como NP-completos, con aplicaciones en múltiples disciplinas.
Aplicaciones de los Problemas NP-Completos en la Industria
Aunque la teoría de la complejidad pueda parecer abstracta, los problemas NP-completos tienen implicaciones prácticas en el mundo real. Aquí algunas de sus aplicaciones más destacadas:
- Ciberseguridad y Criptografía: Muchos sistemas de encriptación dependen de problemas difíciles de resolver en tiempo polinómico, como la factorización de números primos (base de RSA).
- Inteligencia Artificial: El aprendizaje automático y la planificación en IA a menudo involucran la resolución de problemas NP-completos, como la optimización de redes neuronales.
- Optimización y Logística: Empresas como Amazon y UPS dependen de algoritmos heurísticos y aproximaciones para resolver problemas como el TSP, maximizando la eficiencia en la distribución de paquetes.
El estudio de estos problemas es fundamental porque nos ayuda a comprender los límites de la computación. Si algún día se demuestra que P = NP, se revolucionarían áreas como la seguridad informática y la inteligencia artificial. Sin embargo, hasta el momento, este sigue siendo uno de los problemas abiertos más importantes de las matemáticas.
Los problemas NP-completos están en el corazón de la informática teórica y aplicada, desafiando los límites del conocimiento computacional. Comprenderlos es clave para desarrollar algoritmos más eficientes y explorar nuevas soluciones a problemas complejos en diversos campos. Si quieres dominar el análisis de datos y la resolución de problemas computacionales avanzados, el Bootcamp de Big Data y Machine Learning de KeepCoding te proporcionará las herramientas necesarias para enfrentarte a los retos del procesamiento masivo de datos, la optimización algorítmica y la inteligencia artificial, preparándote para un futuro tecnológico lleno de oportunidades.











