La regresión lineal múltiple en estadística Big Data es uno de los múltiples cálculos que se implementan en el desarrollo de un estudio estadístico con respecto al comportamiento de las diferentes variables que se abordan. Por ello, resulta de suma importancia saber cómo funciona y en qué momento un estadístico es necesario para potenciar los resultados arrojados en el procesamiento de los datos.
Por otra parte, para considerar este cálculo, debes tener en cuenta cuáles son las variables que serán estudiadas en el estudio estadístico y cuáles son las relaciones que se establecen entre estas. Por este motivo, en este post, te presentamos qué es la regresión lineal múltiple en estadística Big Data.
Regresión lineal múltiple en estadística Big Data
Hasta ahora habrás visto cómo el cambio en una variable puede afectar a otra, pero ¿qué ocurre si son varias las variables que alteran el comportamiento de la variable objetivo?
Pues bien, para este caso necesitarás utilizar la regresión lineal múltiple en estadística Big Data. Este, en definitiva, es un modelo matemático usado para aproximar la relación de dependencia entre una variable dependiente Y, las variables independientes X y un término aleatorio ε.
Por otra parte, este modelo de regresión lineal múltiple en estadística Big Data puede ser expresado con la siguiente fórmula:
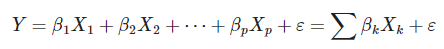
En la que podrás encontrar:
- Y: la variable dependiente.
- X1, X2, …, Xp: las variables independientes.
- β0, β1, β2, …, βp: los parámetros que determinan que dado un Xk produce el mejor posible Y.
- ε: el error o valor aleatorio.
Condiciones para aplicarlo
- Que la relación entre las variables sea lineal.
- Que los errores en la medición de Xk sean independientes entre sí.
- Que los errores tengan una varianza constante.
- Que los errores tengan una media aritmética igual a cero.
Ahora bien, para la regresión lineal múltiple en estadística Big Data es necesario calcular el valor óptimo de β. Para ello, vas a tener que utilizar un poco de álgebra lineal, así:
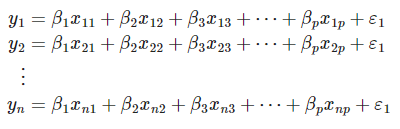
De igual forma, este cálculo también podrás escribirlo en forma de matriz: [ \begin{bmatrix} y_1 \ y_2 \ \vdots \ y_n.
\end{bmatrix}
Este tipo de matriz es de suma importancia en el cálculo de la regresión lineal múltiple en estadística Big Data y se presenta de la siguiente forma:
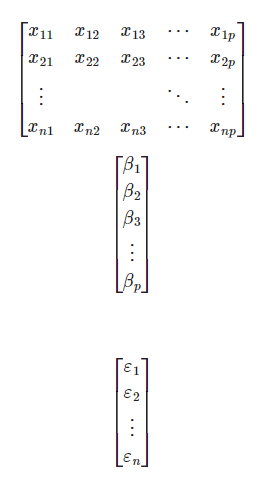
/] Lo que se puede simplificar como:
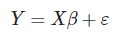
Al igual que en el caso anterior, podrás estimar β con:
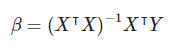
Esto se lleva a cabo en el siguiente proceso de inscripción:
n<-10
x1<-rep(1,n)
x2<-seq(2,to=11,length.out = n)
x3<-seq(0.3,to=5,length.out = n)^2
X<-matrix(c(x1,x2,x3),nrow=n,byrow = F)
print("El valor de la matriz X es:")
X
beta<-matrix(c(5,2,14),nrow=3)
print("El valor de la matriz Y es:")
Y<-X %*% beta+rnorm(n)
Y
[1] “El valor de la matriz X es:”
A matrix: 10 × 3 of type dbl
| 1 | 2 | 0.0900000 |
| 1 | 3 | 0.6760494 |
| 1 | 4 | 1.8075309 |
| 1 | 5 | 3.4844444 |
| 1 | 6 | 5.7067901 |
| 1 | 7 | 8.4745679 |
| 1 | 8 | 11.7877778 |
| 1 | 9 | 15.6464198 |
| 1 | 10 | 20.0504938 |
| 1 | 11 | 25.0000000 |
[1] “El valor de la matriz Y es:”
A matrix: 10 × 1 of type dbl
| 9.932899 |
| 18.895609 |
| 37.937981 |
| 65.146657 |
| 96.560780 |
| 138.376701 |
| 186.975475 |
| 242.054275 |
| 305.354591 |
| 376.470304 |
print("El valor estimado de beta es:")
est_beta<-solve(t(X) %*% X) %*% t(X) %*% Y
est_beta
print("El valor real de beta es:")
beta
[1] “El valor estimado de beta es:”
A matrix: 3 × 1 of type dbl
| 2.550833 |
| 2.709907 |
| 13.761831 |
[1] “El valor real de beta es:”
A matrix: 3 × 1 of type dbl
| 5 |
| 2 |
| 14 |
En la regresión lineal múltiple en estadística Big Data, esto también se puede resolver con la función lm de R. De manera que se ignora el vector x1 porque la función por defecto ya añade el término.
lm(Y~x2+x3)
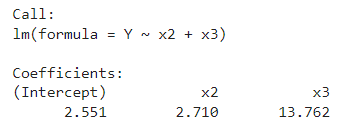
Aprende sobre la regresión lineal múltiple en estadística Big Data
En el transcurso de este post, te has podido familiarizar con todo a lo que hace referencia a la regresión lineal múltiple en estadística Big Data, gracias a unos conocimientos teóricos y prácticos que debes tener en cuenta una vez te enfrentes a este tipo de cálculo en tu procesamiento de los macrodatos. Sin embargo, ¡todavía falta mucho por aprender de este tipo de estadístico!
Por esta razón, desde KeepCoding te ofrecemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. A través de esta formación intensiva, podrás familiarizarte con un ecosistema de desarrollo, conocer un IDE profesional y profundizar sobre el lenguaje de programación nativo Big Data Scala, ya que con este se ha escrito uno de los motores de procesamiento más conocidos hasta la fecha, Apache Spark. ¡Apúntate ya y sé un experto del Big Data en menos de nueve meses!







