Regularización de un algoritmo de reconocimiento facial

En este post realizaremos la regularización de un algoritmo con el que hemos estado trabajando en otros artículos con un ejercicio de reconocimiento facial y el algoritmo Eigenfaces.

Recordemos que la regularización de un algoritmo en R es una técnica aplicada en la precisión de los modelos de entrenamiento, lo cual influye en que se creen modelos más simples y entendibles sobre un conjunto de datos determinado.

Existen diferentes tipos de regularización: la regularización Lasso o L, la regularización Ridge o L² y la regularización elástica, que es una mezcla de las dos anteriores.

Regularización de un algoritmo

Podemos utilizar la regularización de un algoritmo con modelos GLM. Veamos:

#Regularización de un algoritmo
number_of_pca_components <- 150

df_train <- data.frame (pr_pics$x [ , 1 : number_of_pca_components])
df_trainsname <- as.factor (rownames (pr_pics$x))
head (df_train)

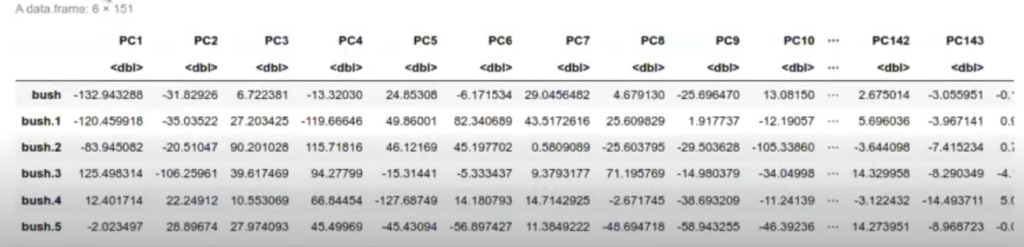
El glmnet corresponde a la regularización. En un artículo anterior veíamos cómo funcionaban las regularizaciones Ridge o Lasso, en las que le imponíamos una penalización a nuestros coeficientes para que nos cogiera solo los coeficientes más pequeños. Esto lo que hacía era evitar que los coeficientes crecieran demasiado.

El glmnet en vez de minimizar la función de coste de la regularización Ridge, lo que hace es minimizar la función de la regularización elástica, es decir:

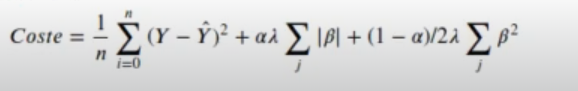
Esta función tiene dos variables, ya que el alpha nos indica que va entre 0 y 1. Recordemos que si el alpha es 1, estamos en la regularización Lasso y, en nuestro caso, como alpha es 1, tenemos esta regularización de Lasso.

Este algoritmo lo que hace es calcular cuál es el beta lambda más óptimo, que minimice el error. Entonces, como no tiene un valor de testing, ya que solo le estamos dando un valor de training, se dividía a sí mismo en varios grupos de test y training. Creaba varios grupos, donde siempre dejaba uno para testing y el resto para training. Luego, hacía varias regresiones lineales internamente y nos daba una medida del error, que es la línea roja que aparece en la gráfica.

Ese error es el error que él está midiendo con ese valor de testing que se ha guardado y esto es lo que nos da el valor de lambda.

Entonces, ese valor de lambda mínimo es el que luego utilizamos para la predicción.

#Regularización de un algoritmo
#model <- glm (dr_train, formula = "name~", family = binomial)
cvfit <- glmnetUtils :: cv.glmnet (name~., family = "binomial",
data = df_train, nfolds = 10, alpha = 1)
plot (cvfit)

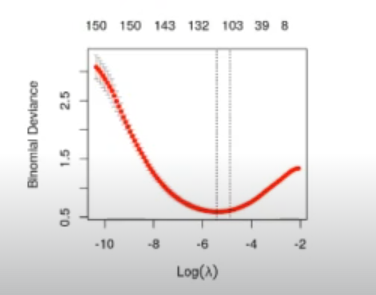
Después, cuando llegamos al método de test, usamos el predict primero para transformar al dominio PCA, pero luego usamos el predict de la regresión lineal y logística.

Le estamos pasando allí, en el anterior cálculo, el lambda que hemos calculado antes.

#Regularización de un algoritmo
test_pics_pca <- predict (pr_pics, test_matrix)
df_test <- data.frame (test_pics_pca [ , 1 : number_of_pca_components])
df_test$name <- as.factor (rownames (test_pics_pca))
p <- predict (cvfit, newdata = df_test, s = cvfit$lambda.min)
pr <- prediction (p, df_test$name]
prf_auc = performance (pr, measure = "auc")
paste ( "The AUC is", prf auc@y. values [[1]])

‘The auc is 0.934458788480636’

El auc aquí es un poco más alto.

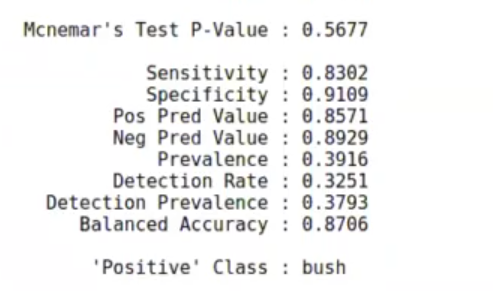
Para medir la calidad, podemos sacar la matriz de confusión.

df_result$pred_name <- as.factor (ifelse (p < 0, 'bush', 'other'))
confusionMatrix (table (df_result$pred_name, df_result$_real))

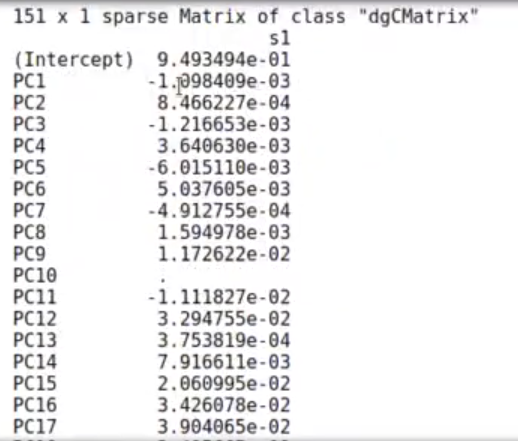
Como valor adicional, tenemos los coeficientes. Por ejemplo, vemos que el coeficiente 10 no lo ha usado, el del 41 tampoco y lo mismo el del 43. Estos componentes los descarta, ya que no son tan importantes.

Aunque bien es cierto que no hay correlación entre los elementos, entre cada uno de los componentes, sí puede ser que estén un poco relacionados con un componente principal y otro que tenga valores más altos en el caso de que, de acuerdo a nuestro ejemplo, aparezca la foto de George Bush.

coef (cvfit, s = cvfit$lambda.min)

Ahora que has visto este tema, ¿qué te parece si seguimos aprendiendo? Recuerda que por medio de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp obtienes una formación intensiva en la que adquirirás todos los conocimientos necesarios para incursionar en el mercado laboral y seguir creciendo profesional y personalmente. ¡Anímate a impulsar tu vida y solicita más información!