La regularización por Dropout en red convolucional es uno de los tipos de regularización que podrás encontrar dentro del Deep Learning. Por ello, en este post, te explicamos cómo funciona la regularización por Dropout en red convolucional.
Regularización por Dropout en red convolucional
La regularización por Dropout en red convolucional es una técnica desarrollada por Srivastava y otros en su artículo Dropout: A Simple Way to Prevent Neural Networks from Overfitting, que complementa los otros tipos de normalización (L1, L2, maxnorm).
Es una técnica extremadamente efectiva y simple que consiste en mantener una neurona activa o ponerla a 0 durante el entrenamiento con una probabilidad p.
Lo que hace la regularización por Dropout en red convolucional es cambiar la arquitectura de la red en tiempo de entrenamiento, lo que significa que no habrá una sola neurona responsable de activarse ante un determinado patrón, sino que tendremos múltiples neuronas redundantes capaces de reaccionar ante ese patrón.
Ejemplo práctico de regularización por Dropout
Veamos qué tal se porta nuestra red con Dropout:
# Prueba con Dropout
# importamos la capa Dropout
from tensorflow.keras.layers import Dropout
# Inizializamos el modelo
model = Sequential()
# Definimos una capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(Dropout(0.25))
# Definimos una segunda capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model.add(Dropout(0.25))
# Definimos la tercera capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model.add(Dropout(0.25))
# Añadimos nuestro clasificador
model.add(Flatten())
model.add(Dense(1024, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
# Compilamos el modelo
model.compile(loss='categorical_crossentropy',
optimizer=Adam(lr=0.0001, decay=1e-6),
metrics=['accuracy'])
# Entrenamos el modelo
model.fit(X_train_norm, to_categorical(Y_train),
batch_size=128,
shuffle=True,
epochs=10,
validation_data=(X_test_norm, to_categorical(Y_test))) # aquí deberíamos usar un conjunto distinto al de test
# Evaluamos el modelo
scores = model.evaluate(X_test_norm, to_categorical(Y_test))
print('Loss: %.3f' % scores[0])
print('Accuracy: %.3f' % scores[1])
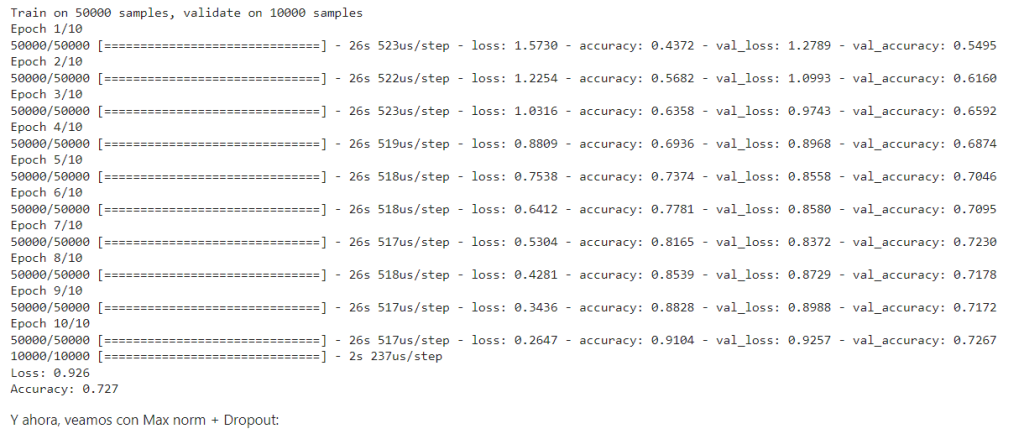
# Prueba con Dropout y Maxnorm
from tensorflow.keras.constraints import max_norm
from tensorflow.keras.layers import Dropout
# Inizializamos el modelo
model = Sequential()
# Definimos una capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(Dropout(0.25))
# Definimos una segunda capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model.add(Dropout(0.25))
# Definimos una tercera capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model.add(Dropout(0.25))
# Añadimos nuestro clasificador
model.add(Flatten())
model.add(Dense(1024, activation='relu', kernel_constraint=max_norm(3.)))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
# Compilamos el modelo
model.compile(loss='categorical_crossentropy',
optimizer=Adam(lr=0.0001, decay=1e-6),
metrics=['accuracy'])
# Entrenamos el modelo
model.fit(X_train_norm, to_categorical(Y_train),
batch_size=128,
shuffle=True,
epochs=10,
validation_data=(X_test_norm, to_categorical(Y_test))) # aquí deberíamos usar un conjunto distinto al de test
# Evaluamos el modelo
scores = model.evaluate(X_test_norm, to_categorical(Y_test))
print('Loss: %.3f' % scores[0])
print('Accuracy: %.3f' % scores[1])
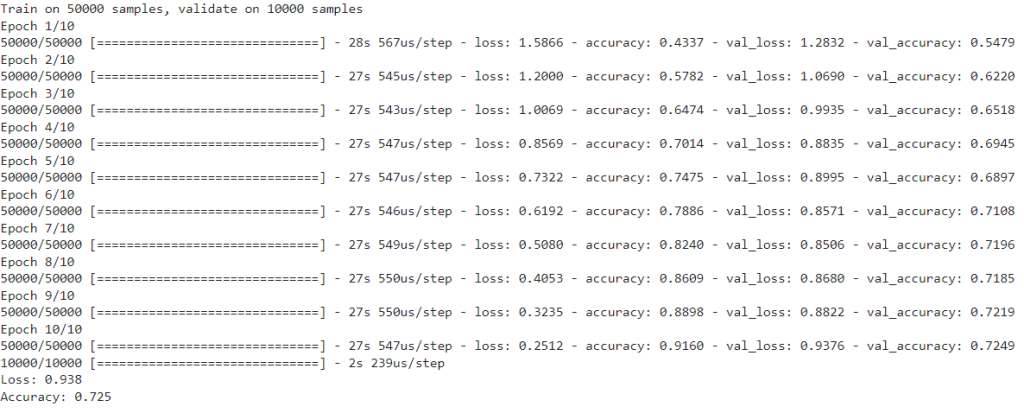
¿Y si usásemos, además, la capa MaxPooling?
# Prueba con Dropout, Maxnorm y Maxpooling
from tensorflow.keras.layers import Dropout
from tensorflow.keras.constraints import max_norm
from tensorflow.keras.layers import MaxPooling2D
# Inizializamos el modelo
model = Sequential()
# Definimos una capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
# Definimos la segunda capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
# Definimos una tercera capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
# Añadimos nuestro clasificador
model.add(Flatten())
model.add(Dense(1024, activation='relu', kernel_constraint=max_norm(3.)))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
# Compilamos el modelo
model.compile(loss='categorical_crossentropy',
optimizer=Adam(lr=0.0001, decay=1e-6),
metrics=['accuracy'])
# Entrenamos el modelo
model.fit(X_train_norm, to_categorical(Y_train),
batch_size=128,
shuffle=True,
epochs=10,
validation_data=(X_test_norm, to_categorical(Y_test))) # aquí también deberíamos usar un conjunto distinto al de test
# Evaluamos el modelo
scores = model.evaluate(X_test_norm, to_categorical(Y_test))
print('Loss: %.3f' % scores[0])
print('Accuracy: %.3f' % scores[1])
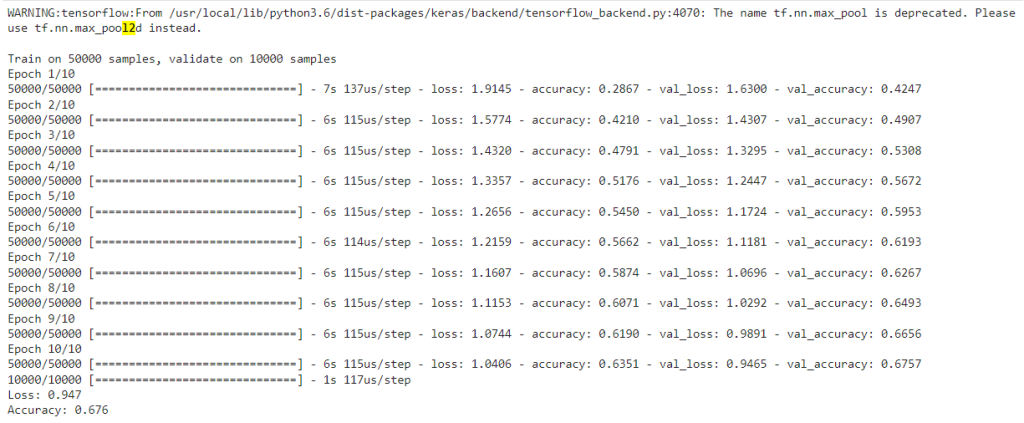
¿Y aumentando el strides a (2,2) en las convolucionales, en vez de añadir MaxPooling?
# Prueba con Dropout, Maxnorm y strides = 4 en las convolucionales
from tensorflow.keras.constraints import max_norm
from tensorflow.keras.layers import Dropout
# Inizializamos el modelo
model = Sequential()
# Definimos una capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), strides=(2,2), activation='relu', input_shape=(32, 32, 3)))
model.add(Dropout(0.25))
# Definimos una segunda capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), strides=(2,2), activation='relu'))
model.add(Dropout(0.25))
# Definimos una tercera capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), strides=(2,2), activation='relu'))
model.add(Dropout(0.25))
# Añadimos nuestro clasificador
model.add(Flatten())
model.add(Dense(1024, activation='relu', kernel_constraint=max_norm(3.)))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
# Compilamos el modelo
model.compile(loss='categorical_crossentropy',
optimizer=Adam(lr=0.0001, decay=1e-6),
metrics=['accuracy'])
# Entrenamos el modelo
model.fit(X_train_norm, to_categorical(Y_train),
batch_size=128,
shuffle=True,
epochs=10,
validation_data=(X_test_norm, to_categorical(Y_test))) #recuerda usar un conjunto distinto al de test
# Evaluamos el modelo
scores = model.evaluate(X_test_norm, to_categorical(Y_test))
print('Loss: %.3f' % scores[0])
print('Accuracy: %.3f' % scores[1])
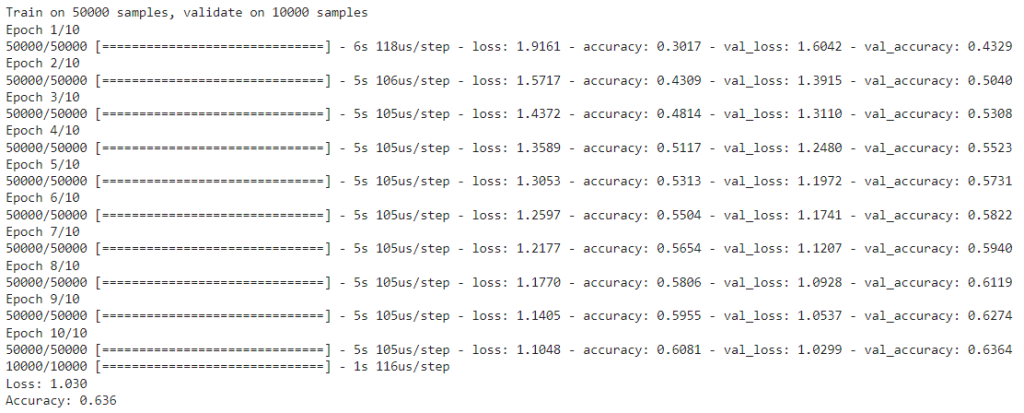
Los resultados son parecidos en términos de velocidad, pero la precisión es menor. En un artículo publicado en 2014, los autores proponían dejar de usar las capas de pooling en pro de la simplicidad, y de hecho, hay arquitecturas como la ResNet que abogan por esto. Sin embargo, siguen utilizándose bastante a día de hoy en la regularización por Dropout en red convolucional.
Aprende más sobre el Big Data
En este post, te hemos expuesto todo sobre la regularización por Dropout en red convolucional, sin embargo, si quieres aprender más sobre el manejo del Big Data, desde KeepCoding te brindamos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. Al finalizar esta formación, en menos de nueve meses, serás capaz de reconocer las ventajas e inconvenientes de los distintos programas estudiados. ¡Inscríbete!











