Regularización L1 en red neuronal convolucional es una de las diferentes alternativas con las que podrás contar para el desarrollo Deep Learning en un procesamiento del Big Data. En suma, este tipo de regularización en red neuronal convolucional es la más utilizada, por lo que conocerla es de suma importancia para un buen data scientist.
Por esta razón, en este post, te explicamos qué es y cómo funciona la regularización L1 en red neuronal convolucional.
Regularización L1 en red neuronal convolucional
La regularización L1 en red neuronal convolucional es bastante común, de hecho, es una de las más utilizadas. En esta ocasión, añadimos el término λ|w| a nuestra función de pérdidas.
También podemos combinar la regularización L1 en red neuronal convolucional con la L2 en lo que se conoce como Elastic net regularization: λ1|w|+12λ2w2.
La regularización L1 en red neuronal convolucional consigue convertir la matriz de pesos W en una matriz de pesos dispersa o sparse (muy cercana a cero, excepto por unos pocos elementos).
Esto implica que, al revés de lo que sucede con L2, lo que se consigue es dar mucha más importancia a unas neuronas que a otras, con lo que la red se convierte en más robusta frente a posible ruido.
Por lo general, si no estás muy seguro, la L2 suele dar mejores resultados. La L1 la puedes usar si tienes imágenes en las que sabes que hay un número determinado de características que te van a dar una buena clasificación y no quieres que la red se fije en el ruido.
Ejemplo práctico de regularización L1 en red neuronal convolucional
Probemos con la regularización L1 en red neuronal convolucional y, después, con la L1+L2:
# Prueba con regularización L1
# importamos la capa regularización
from keras.regularizers import l1
# Inizializamos el modelo
model = Sequential()
# Definimos una capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu', input_shape=(32, 32, 3)))
# Definimos una segunda capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
# Definimos una tercera capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
# Añadimos nuestro clasificador
model.add(Flatten())
model.add(Dense(1024, activation='relu', kernel_regularizer=l1(0.01)))
model.add(Dense(10, activation='softmax'))
# Compilamos el modelo
model.compile(loss='categorical_crossentropy',
optimizer=Adam(lr=0.0001, decay=1e-6),
metrics=['accuracy'])
# Entrenamos el modelo
model.fit(X_train_norm, to_categorical(Y_train),
batch_size=128,
shuffle=True,
epochs=10,
validation_data=(X_test_norm, to_categorical(Y_test))) # aquí deberíamos usar un conjunto distinto al de test!!!
# Evaluamos el modelo
scores = model.evaluate(X_test_norm, to_categorical(Y_test))
print('Loss: %.3f' % scores[0])
print('Accuracy: %.3f' % scores[1])
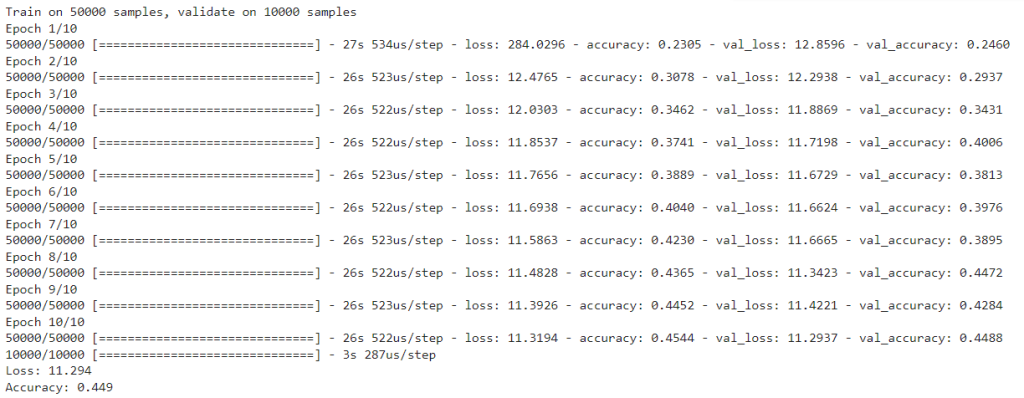
# Prueba con regularización elástica (L1 + L2, Elastic net regularization)
# importamos la capa regularización
from tensorflow.keras.regularizers import l1_l2
# Inizializamos el modelo
model = Sequential()
# Definimos una capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu', input_shape=(32, 32, 3)))
# Definimos una segunda capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
# Definimos una tercera capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))
# Añadimos nuestro clasificador
model.add(Flatten())
model.add(Dense(1024, activation='relu', kernel_regularizer=l1_l2(0.01, 0.01)))
model.add(Dense(10, activation='softmax'))
# Compilamos el modelo
model.compile(loss='categorical_crossentropy',
optimizer=Adam(lr=0.0001, decay=1e-6),
metrics=['accuracy'])
# Entrenamos el modelo
model.fit(X_train_norm, to_categorical(Y_train),
batch_size=128,
shuffle=True,
epochs=10,
validation_data=(X_test_norm, to_categorical(Y_test))) # aquí deberíamos usar un conjunto distinto al de test!!!
# Evaluamos el modelo
scores = model.evaluate(X_test_norm, to_categorical(Y_test))
print('Loss: %.3f' % scores[0])
print('Accuracy: %.3f' % scores[1])
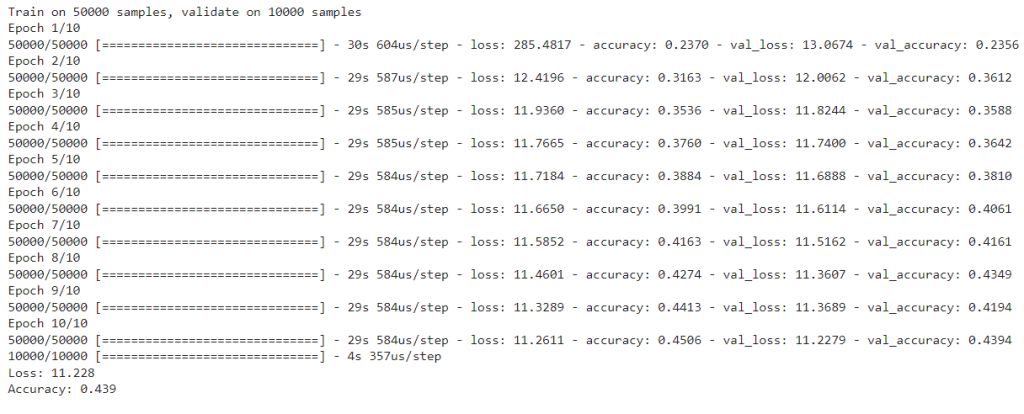
En este post, te hemos familiarizado con la regularización L1 en red neuronal convolucional, no obstante, sabemos que aún queda más por conocer sobre el manejo del Big Data. Por ello, desde KeepCoding te brindamos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, por medio del que te formarás en el proceso de ingesta, clasificación, resguardo, procesamiento y presentación de los macrodatos gracias al uso de diferentes herramientas, sistemas y lenguajes.
En el transcurso de esta formación intensiva de gran calidad, grandes profesionales te ayudarán a tener una visión global del mundo Big Data, entonces, serás capaz de reconocer las ventajas e inconvenientes de los distintos programas estudiados. ¡Echa un vistazo a nuestro temario e inscríbete ahora!











