La regularización L2 en red neuronal convolucional forma parte de los tipos de regularización en redes neuronales convolucionales para el manejo de las redes neuronales profundas convolucionales dentro del campo del Deep Learning; de hecho, este es el tipo más común de regularización.

De manera que, si te encuentras trabajando con estas redes, debes considerar primero esta alternativa para la generalización de datasets. Por ello, en este post, te compartimos qué es la Regularización L2 en red neuronal convolucional.

Regularización L2 en red neuronal convolucional

La regularización L2 en red neuronal convolucional es, muy seguramente, la más utilizada y común dentro del campo del Deep Learning para la generalización de redes. Esto se debe a que la regularización L2 en red neuronal convolucional consiste en penalizar la función de pérdidas añadiendo el término 12λw2 para cada peso, lo que resulta en 12λ∑i∑jwi,j2.

Es decir, el 12 es simplemente por términos de comodidad cuando calculamos las derivadas, ya que, de esta forma, nos queda λw en vez de 2λw. Lo que quiere decir esto es que penalizamos los pesos muy altos o dispares y preferimos que sean todos ellos de magnitudes parecidas.

Ahora, has de recordar que lo que implican los pesos es la importancia de cada neurona en el cómputo final de la predicción. Por lo tanto, haciendo esto conseguimos que todas las neuronas importen más o menos por igual, es decir, que la red usará todas sus neuronas para hacer la predicción.

Por el contrario, si existiesen pesos muy altos para determinadas neuronas, el cálculo de la predicción tendría mucho más en cuenta a estas, por lo que acabaríamos con una red con neuronas muertas que no sirven para nada.

Además, en la regularización L2 en red neuronal convolucional introducir el término 12λw2 en nuestra función de pérdidas hace que durante el descenso del gradiente se intente aproximar los pesos a cero, decayendo linealmente: W+=−λ⋅W.

Vamos a ver si conseguimos mejorar nuestra red aplicando la regularización L2:

# Regularización L2 en red neuronal convolucional

# importamos la capa regularización
from tensorflow.keras.regularizers import l2

# Inizializamos el modelo
model = Sequential()

# Definimos una capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu', input_shape=(32, 32, 3)))

# Definimos la segunda capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))

# Definimos la tercera capa convolucional
model.add(Conv2D(128, kernel_size=(3, 3), activation='relu'))

# Añadimos nuestro clasificador
model.add(Flatten())
model.add(Dense(1024, activation='relu', kernel_regularizer=l2(0.01)))
model.add(Dense(10, activation='softmax'))

# Compilamos el modelo
model.compile(loss='categorical_crossentropy',
              optimizer=Adam(lr=0.0001, decay=1e-6),
              metrics=['accuracy'])

# Entrenamos el modelo
model.fit(X_train_norm, to_categorical(Y_train),
          batch_size=128,
          shuffle=True,
          epochs=10,
          validation_data=(X_test_norm, to_categorical(Y_test))) # aquí deberíamos usar un conjunto distinto al de test!!!

# Evaluamos el modelo
scores = model.evaluate(X_test_norm, to_categorical(Y_test))

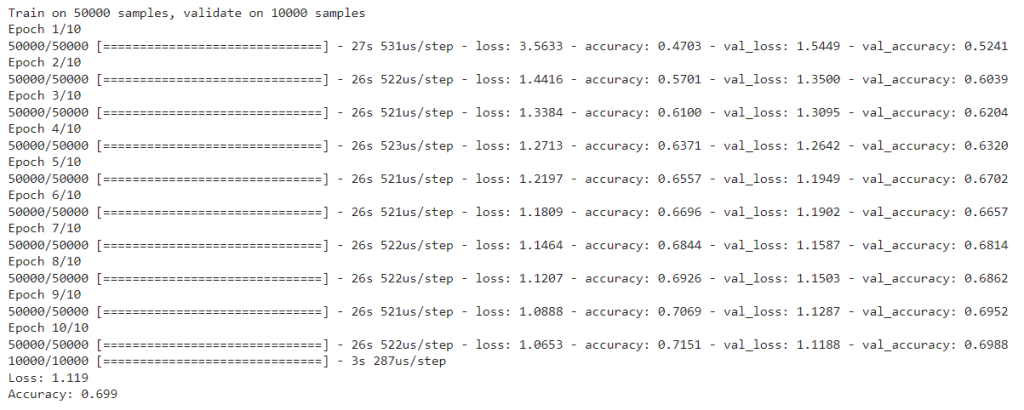
print('Loss: %.3f' % scores[0])
print('Accuracy: %.3f' % scores[1])

En el desarrollo de este post, te hemos compartido qué es y cómo funciona la regularización L2 en red neuronal convolucional, así que ahora solo queda llevarlo a la práctica. De hecho, si planeas continuar aprendiendo sobre el Big Data, desde KeepCodging te traemos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning.

Por medio de esta formación, podrás aprender mucho más sobre los sistemas y herramientas más importantes en el universo del Big Data. De la mano de profesionales y en menos de nueve meses, te convertirás en todo un experto y serás capaz de conocer e identificar las alternativas de gestión de datos más apropiadas para los estudios de los macrodatos. ¡No dudes en solicitar más información e inscríbete ahora!