En este post veremos cómo funciona la regularización sobre algoritmos de clasificación.
Regularización sobre algoritmos de clasificación
Algunos algoritmos de clasificación también tienen un parámetro que permite controlar su complejidad. En el caso de regresión logística, la función de coste a minimizar es:
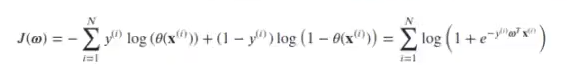
En la que:
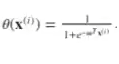
En su versión regularizada, la función de coste pasa a ser:
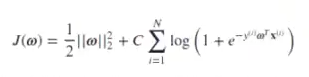
El parámetro que decide cuánto vamos a regularizar es C, que es la inversa de la fuerza de regularización. Este valor de C tiene que ser positivo.
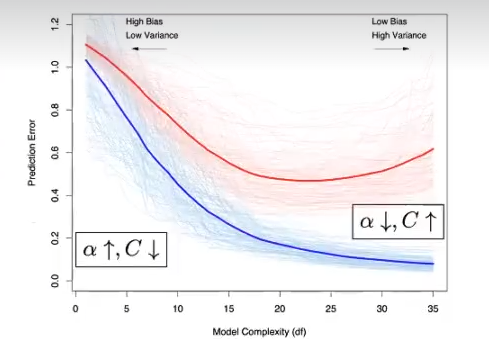
El coste C es el parámetro libre que permite controlar la complejidad del algoritmo, penalizando los errores que se cometen en la clasificación. Este parámetro supone un compromiso entre la exactitud de la solución y la complejidad del algoritmo; en ese sentido, es similar al parámetro de regularización a que utilizamos en Ridge y Lasso. En este caso, de forma intuitiva, podemos decir que C se comporta como l / α. Así:
- Cuanto mayor es C (menor es a), más penalizamos los errores en clasificación y la frontera se ajusta mucho a los datos (en el caso extremo se ajustará perfectamente). Riesgo de overfitting, pero con potencial menor error de clasificación.
- Cuanto menor es C (mayor es a), menos penalizamos los errores en clasificación y tenderemos hacia modelos más sencillos (fronteras menos ajustadas, menor riesgo de overfitting, pero potencialmente con más error de clasificación).
Ten en cuenta que, por defecto, C = 1 en scikit-learn.
Regularización sobre algoritmos de clasificación: ejercicio
#Regularización sobre algoritmos de clasificación
#ejemplo1
ejemplo1 = pd.read_csv ("./data/ex2datal.txt", sep = " , ", header = None, names = ['x1', 'x2', 'label'])
#Regularización sobre algoritmos de clasificación
#ejemplo2
ejemplo2 = pd.read_csv ("./data/ex2data2.txt", sep = " , ", header = None, names = ['x1', 'x2', 'label'])
#Regularización sobre algoritmos de clasificación
#ejemplo 3: Problema KOR
np.random.seed (0)
#parameters
N = 800
mu =1.5 #Cambia este valor
sigma = 1 #Cambia este valor
#variables auxiliares
unos = np.ones (int (N/4))
random4 = sigma * np.random.randn (int (N/4), 1)
random2 = sigma * np.random.randn (int (N/2), 1)
#features
y3 = np.concatenate ([-1 + unos, unos, -1 * unos])
X1= np.concatenate ([-mu + random4, mu + random4, -mu + random4, mu + random4])
X2 = np.concatenate ([ + mu + random2, -mu + random2])
X3 = np.hstack ((X1, X2))#Regularización sobre algoritmos de clasificación
plt.figure (figsize = (15, 5))
plt.subplot (1, 3, 1)
plt.scatter (ejemplo1 ['x1'], ejemplo1 ['x2'], c = ejemplo1 ['label'], cmap = cm_bright)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x 2$", fontsize = 16)
plt.title ('Ejemplo 1')
plt.subplot (1, 3, 2)
plt.scatter (ejemplo2 ['x1'], ejemplo2 ['x2'], c = ejemplo2 ['label'], cmap = cm_bright)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x 2$", fontsize = 16)
plt.title ('Ejemplo 2')
plt.subplot (1, 3, 3)
plt.scatter (X3 [:0], x3 [ : , 1], c = y3, cmap = cm_bright)
plt.xlabel ("$x 1$", fontsize = 16)
plt.ylabel ("$x 2$", fontsize = 16)
plt.title ('Ejemplo 3')
plt.tight_layout ()
plt.show ()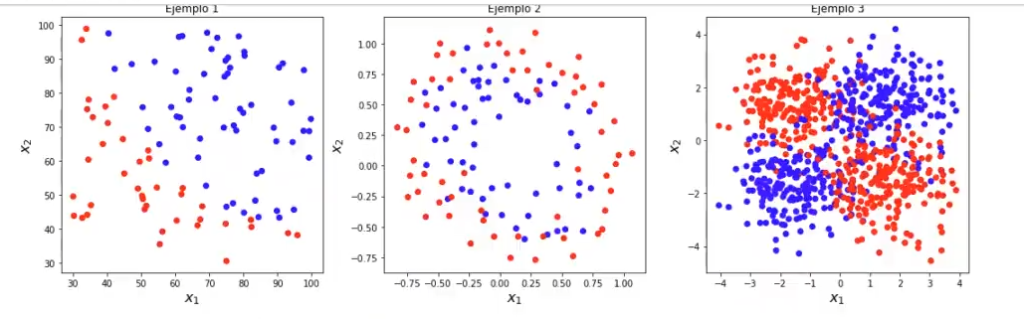
Importamos la regresión logística, así como las métricas. Posteriormente, preparamos los datos y creamos el modelo de regresión logística; a este modelo no le estamos pasando ningún parámetro, por lo que sabemos cuánto va a ser, C = 1, que es el valor por defecto. Por último, ajustamos con los datos disponibles y ejecutamos:
#Regularización sobre algoritmos de clasificación
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
#preparamos los datos
data1 = ejemplo1.values
X1 = data1 [ : , 0 : 2]
y1 = data1 [ : , - 1]
#creamos el modelo
lr1 = LogisticRegression () #C = 1.0 (valor por defecto)
#ajustamos con los datos disponibles
lri.fit(x1, y1)
plot_decision_boundary (X1, y1, 0.05, lr1)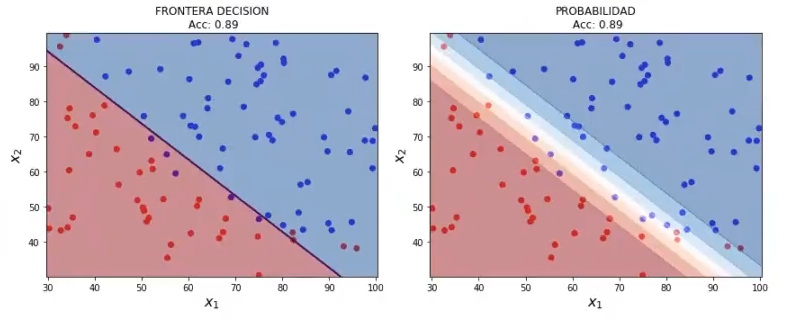
#Regularización sobre algoritmos de clasificación
#C grande (Antes de ejecutar imagina cómo puede ser el resultado)
lr1 = LogisticRegression (C = 1000)
Ir1.fit (x1, y1)
plot_decision_boundary (x1, y1, 0.05, lr1)¿Qué crees que va a pasar con la ejecución de este algoritmo? ¿Qué sucede si C es muy grande? Lo que tendría que pasar es que debería crearse un modelo más complejo y con overfitting. Veamos el resultado:
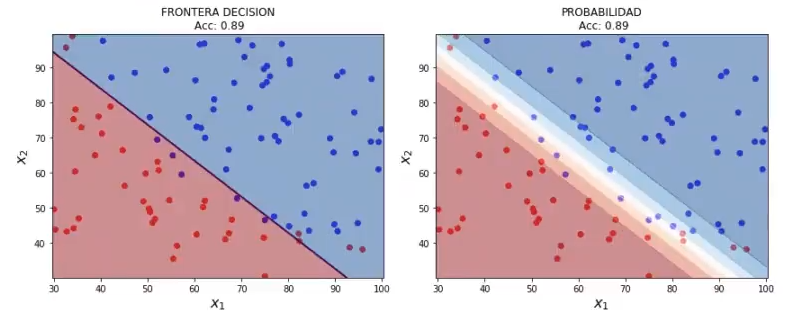
Hemos recibido literalmente lo mismo.
Ahora lo que haremos será bajar C un poco. Lo que debería pasar es que tenemos un modelo más sencillo. Veamos:
#Regularización sobre algoritmos de clasificación
#C pequeño
lr1 = LogisticRegression (C = 0.4)
Ir1.fit (x1, y1)
plot_decision_boundary (x1, y1, 0.05, lr1)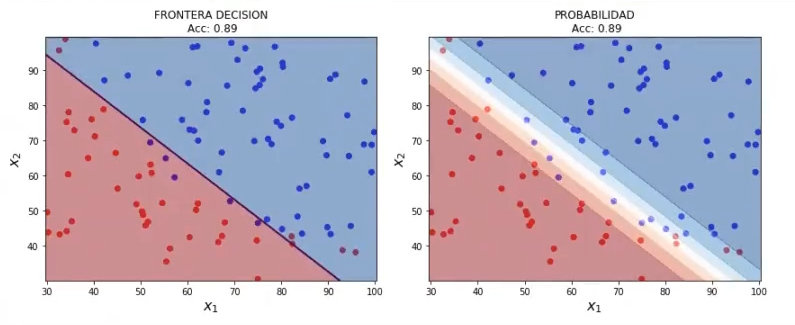
No obstante, hemos recibido lo mismo que en el modelo anterior.
¿Quieres seguir aprendiendo?
Como hemos visto, en los tres ejemplos de C vemos el mismo resultado. Si quieres entender por qué sucede esto, tenemos una oferta para ti: en el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp podrás aprender esto y mucho más. Esta es una formación intensiva en la que adquirirás todos los conocimientos teóricos y prácticos para incursionar en un mercado laboral lleno de oportunidades. ¡Anímate a transformar tu futuro y solicita más información ahora!











