En este artículo vamos a ver cómo funciona la regularización sobre algoritmos de regresión.
Trabajaremos la regularización Lasso y la regularización Ridge, L1 y L2, respectivamente.
Pintar las gráficas
Lo primero que haremos es cargar las librerías y las funciones necesarias para pintar las gráficas:
#Regularización sobre algoritmos de regresión
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
%matplotlib inline
cm = plt.cm. RdBu
cm_bright = ListedColormap (['#FF0000', '#0000FF'])
import warnings
warnings.filterwarnings ('ignore')#definimos una función para representar el resultado del ajuste
#Regularización sobre algoritmos de regresión
def plot_decision_boundary (X, y, h, model):
x_min, x_max = X [ : , 0].min () - .5, X [ : , 0].max () + .5
y_min, y_max = X [ : , 1].min () - .5, X [ : , 1].max () + .5
h = .05 #step size in the mesh
xx, yy = np.meshgrid (np.arange (x_min, x_max, h), np.arange (y_min, y_max, h))
Zd = model.predict (np.c [xx.ravel (), yy.ravel ()])
Zd= Zd.reshape (xx.shape)
Zp = model.predict proba (np.c_ [xx.ravel), yy.ravel ()]) [ : ,1]
Zp = Zp.reshape (xx. shape)
#Error de clasificación
ypred = model.predict (x)
acc = accuracy_score (y, ypred)
plt.figure (1, figsize = (12, 5))
plt.subplot (1, 2, 1)
plt.scatter (X [ : , 0], X [ : , 1], c = y, cap = cm_bright)
plt.axis ([x_min, x_max, y_min, y_max])
plt.contour (xx, yy, Zd, levels = [ 0 ], linewidths = 2)
plt.contourf (xx, yy, Zd, cmap = co, alpha = .5)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel("$x 2$", fontsize = 16)
msg = 'FRONTERA DECISION\n Acc: %0.2g' % acc
plt.title (msg)
plt.subplot (1, 2, 2)
plt.scatter (X [ : , 0], X [ : , 1], c = y, cmap = cm_bright)
plt.axis ([x_min, x_max, y_min, y_max])
#plt. contour(xx, yy, Zp, levels = [0], linewidths = 2)
plt.contourf (xx, yy, Zp, cmap = cm, alpha = .5)
plt.xlabel ("$x_1s", fontsize = 16)
plt.ylabel ("$x_2$", fontsize = 16)
msg = 'PROBABILIDAD\n Acc: %0.2g' % acc
plt.title (msg)
plt.tight_layout ()
plt.show ()Regularización sobre algoritmos de regresión
Ahora entendamos mejor cómo funciona la regularización sobre algoritmos de regresión:
#Regularización sobre algoritmos de regresión
N_train = 10
N_test = 100
#función verdadera g (x)
x = np.linspace (0, 1, N_test)
g_x = np.cos (1.5 * np.pi * x)
# proceso y
np.random.seed (0) #para asegurar reproducibilidad
epsilon = np.random.randn (N_test) * 0.2
y = g_x + epsilon
# Datos: 0 = {x_1, y_1}, obtenemos una muestra
#Regularización sobre algoritmos de regresión
idx = np.random.randint (0, N_test, N_train)
x_i = x [idx]
y_i = y lidx]
#dibujamos la función g(x), y el conjunto de datos x_i, y_i
plt.plot (x, g_x, 'r', label = 'g (x) ' )
plt.plot (x_i, y_i, 'b.', label = 'y')
plt.legend ()
plt.show ()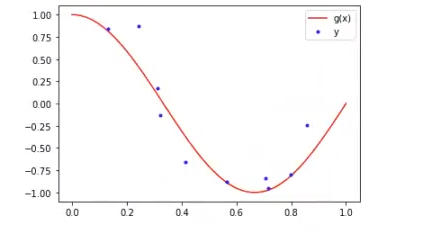
En primer lugar, ajustamos un modelo (regresión lineal) muy complejo sobre estos datos de la siguiente forma:
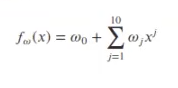
Tiene 10 coeficientes (ω1, … , ω10). Este modelo seguramente sufrirá overfitting.
Ahora lo que haremos será entrenar un algoritmo de regresión lineal y calcular el error cuadrático medio del conjunto de test:
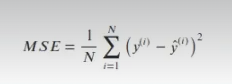
#Regularización sobre algoritmos de regresión
from sklearn.preprocessing import Polynomial Features
from sklearn.linear model import LinearRegression
degree = 10
#features
poly = Polynomial Features (degree) #generamos x^j
X_train = poly. fit_transform (x_i.reshape (-1, 1))
y_train = y_i
X_test = poly.fit_transform (x.reshape (-1, 1))
y_test = y
lr = linearRegression ().fit (X_train, y_train)
#predicción
y_hat = lr.predict (X_test)
mse = np.mean ((y - y_hat) 2)
plt.plot (x, g_x, 'r', label = '$y$')
plt.plot (x_i, y_i, 'b.', label = '$y_i$')
plt.plot (x, y_hat, 'g', label = '$\hat {y} $')
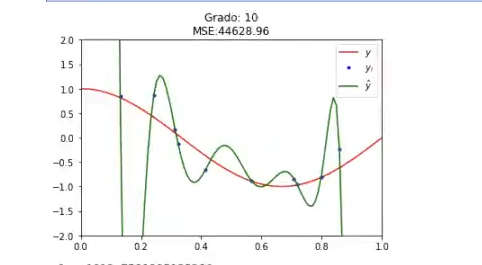
plt.title ('Grado: %i\nMSE:2f'% (degree, mse))
plt.legend ()
plt.xlim ((0, 1))
plt.ylim ((-2, 2))
plt.show ()
#Mostramos los coeficientes del modelo
#Regularización sobre algoritmos de regresión
prin t('w0: ', lr.intercept_)
w = lr.coef_
norm_w2 = np.dot (w, w, T) #no se tiene en cuenta el intercepto
coef_names = ['w' + str (i) + ' : ' for i in range (1, degree + 1)]
for f, wi in zip(coef_names, w):
print (f, wi)
print ('\n l l w l l _2 ^ 2 -- %.2g' % norm_w2)
w0: 1018.7591895935266
w1: -0.029389281292386715
w2: -24032.863921608543
w3: 231294.00705064868
w4: -1191201.1474242613
w5: 3568841.9532320956
w6: -6150955.357541396
w7: 5013085.5819753045
w8: 1032053.2895785227
w9: -5939085.981209873
w10: 4781062.610945556
Mostramos los coeficientes del modelo. Vemos cómo, salvo el primero, que tiene como motivo un -0.029389281292386715, el resto son todos del orden de los millones, es decir, son coeficientes muy altos.
El que tenemos, por lo tanto, es un modelo de una altísima complejidad y está claramente sobreajustado a los datos, es decir, está en overfitting. ¿Qué podemos hacer? Podemos tratar de suavizar este modelo, regularizarlo manteniendo no más que la complejidad inicial, que son los 10°. Vamos a penalizar los coeficientes altos y lo que va a conseguir eso es que el modelo sea mucho más sencillo.
¿Cómo continuar?
El Big Data tiene uno de los mercados laborales más prolíficos del sector IT, por eso, si quieres empezar a ver los resultados de tus esfuerzos, tenemos una excelente opción para ti: por medio de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, podrás aprender todo lo necesario para incursionar en el mundo profesional en pocos meses. ¡Anímate a impulsar tu futuro y solicita ya más información!











