La regularización sobre regresión Ridge se refiere al modelo de regresión lineal con penalización sobre la magnitud de los coeficientes como medida contra el overfitting.

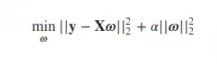
El modelo de regularización sobre regresión Ridge tiene un parámetro libre (α) que hemos de fijar a priori. En otras palabras, tenemos que valorar que el modelo calcule los coeficientes ω. A tener en cuenta:

Si α = 0, el resultado se asemeja a un modelo de regresión lineal. Pero cuidado, porque no será igual, ya que sklearn trata de forma diferente Lasso o Ridge con a = 0 y la regresión lineal.
Si α → ∞, el valor de todos los coeficientes será nulo.
La implementación de scikit learn de un modelo de Ridge es una mezcla de regresión lineal con regularización. Es decir, no hay un modelo Ridge como tal. Lo mismo pasa con Lasso, pero esto es solo en sklearn.

Por tanto, para buscar el valor de α adecuado, tendremos que barrer valores en una escala que cubra valores muy pequeños y valores elevados. Para ello, normalmente se utiliza escala logarítmica aumentando progresivamente el orden de magnitud. Como ejemplo, podríamos barrer lambda utilizando los siguientes valores α = {10^-3, 0.01, 0.1,1,10, 100, 1000}, que en escala logarítmica queda como: log₁₀(α) = {-3, -2, -1, 0, 1, 2, 3}.

Regularización sobre regresión Ridge: ejercicio

Vamos a implementar el algoritmo de Ridge regression variando los valores de α y viendo cómo esta variación afecta a los coeficientes ω del modelo:

#Regularización sobre regresión Ridge
from sklearn.linear_model import Ridge

#model
alpha = 1e - 14
ridge = Ridge (alpha = alpha).fit (X_train, y_train)
w= ridge.coef_
norm_w2 = np.dot (w, w.T)

#predicción
y_hat = ridge.predict (X_test)

#error
#Regularización sobre regresión Ridge
error_test = np.mean (np.power (y - y_hat, 2))

plt.plot (x, g_x, 'r', label = '$y$')
plt.plot (x_i, y_i, 'b.', label = '$y_i$')
plt.plot (x, y_hat, 'g', label ='$\hat {y} $)
plt.title ('Grado: %i, MSE: %.2f\nalpha: %g, $ l l w l l_2 ^ 2$ -- %.2g' % (degree, error_test, alpha, norm_w2)
plt, legend ()
plt.xlim ((0, 1))
plt.ylim ((-2, 2))
plt.show()

coef_names = ['w' + str (i) + ': for i in range (1, degree + 1)]

for f, wi in zip (coef_names, w):
print (f, wi)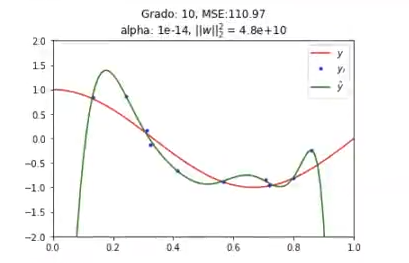

w1: 0.0

w2: 214.71578979492188

w3: -694.8961791992188

w4: -3082.392852783283

w5: 27897.683814697266

w6: -81163.93614196777

w7: 182835.2018737793

w8: -12176.846725463867

w9: -116354.67797851562

w10: 122757.46544647217

Lo que estamos haciendo en el ejercicio anterior es, primero, importar Ridge. Luego, elegiremos un alfa, que en este caso es 1e – 14, y creamos un modelo Ridge con alfa 1e – 14. Ajustamos el modelo a train y test y vemos que prácticamente no sucede nada (gráfica más arriba).

Los coeficientes siguen siendo muy altos porque el parámetro de regularización sobre regresión Ridge es muy bajo.

Entonces, ahora lo que haremos será variar los valores de alfa y comprobar cómo afecta el resultado. ¿Cómo varían los coeficientes del modelo?

Lo que haremos, por tanto, es que en vez de un -14 le pondremos un -10:

#Regularización sobre regresión Ridge
#model
alpha = 1e - 10
ridge = Ridge (alpha = alpha).fit (X_train, y_train)
w= ridge.coef_
norm_w2 = np.dot (w, w.T).

Vamos a quedarnos con la norma de los coeficientes al cuadrado. Con el -14 tenemos un 4.8e + 10. Si ahora lo cambiamos a un -10, el coeficiente al cuadrado ha bajado, estará elevado a 6:

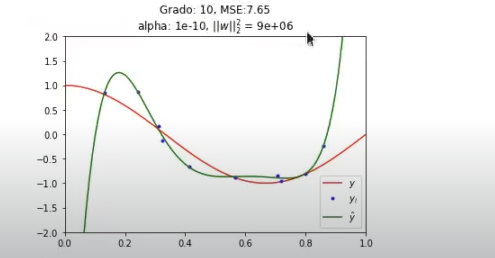
Si lo bajamos aun más y lo ponemos en -5, es decir, si vamos haciendo alfa más grande (vamos regularizando), los coeficientes cada vez son más pequeños. Si subimos alfa un poco más, los coeficientes son más y más pequeños.

#Regularización sobre regresión Ridge
#model
alpha = 1e - 5
ridge = Ridge (alpha = alpha).fit (X_train, y_train)
w= ridge.coef_
norm_w2 = np.dot (w, w.T).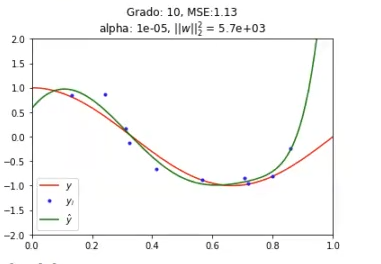

Hay otra cosa más que no hemos comentado y que se va viendo en la progresión de las gráficas: estas se van haciendo cada vez más y más suaves. Esto quiere decir que ha pasado del -14 inicial, que estaba en un claro overfitting, al -10, que sigue en overfitting, pero más suave; y luego al -5, que ya se va ajustando más.

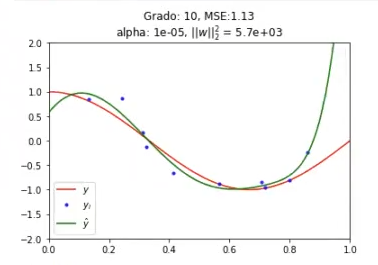
Y por último está el -1:

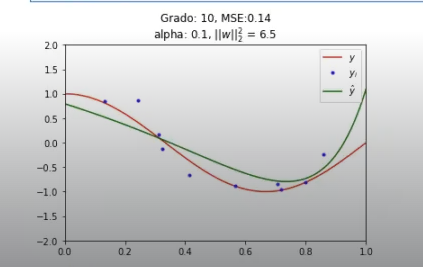
Aquí ya podríamos, incluso, crear un alfa de 1000 y nos quedaría una recta:

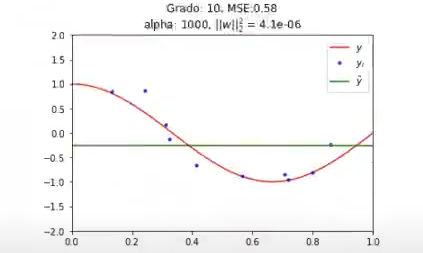
Si te ha gustado este tema y te apasiona el Big Data, no olvides que tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que podrás afianzar tus conocimientos sobre un mundo lleno de oportunidades. Aquí aprenderás todas las herramientas teóricas y prácticas para poder incursionar en el mercado laboral en poco tiempo. ¡Anímate a cambiar tu vida y solicita más información ahora!