Las relaciones entre variables en estadística Big Data forman parte de las estrategias para llevar a cabo un análisis estadístico que destaque el valor de los datos y arroje resultados decisivos para comprender la información. Por ello, en este post, te presentamos cuáles son las relaciones entre variables en estadística Big Data.
¿Cuáles son las relaciones entre variables en estadística Big Data?
Dos variables pueden estar relacionadas entre sí de varias formas. En esta sección vamos a ver cuáles son las relaciones entre variables en estadística Big Data a partir dos variables.
Antes debes tener en cuenta:
La variable Y tiene una variación lineal respecto a X si:
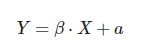
Donde β y α son constantes fijas que definen la relación entre las dos variables. Pero en cambio, no hay una relación lineal en los siguientes casos:
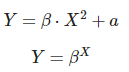
Covarianza
La covarianza es un valor que indica el grado de variación lineal conjunta de dos variables aleatorias respecto a sus medias y es una de las relaciones entre variables en estadística Big Data más empleadas.
Si se comparan dos variables aleatorias X e Y:
- Alta covarianza (positiva): para valores altos de X se cuenten mayoritariamente valores altos de Y.
- Baja covarianza (negativa): para valores altos de X se tenga mayoritariamente valores bajos de Y.
- Covarianza cercana a 0: para valores altos de X, los valores de Y pueden ser altos o bajos por igual.
Su fórmula es la siguiente:
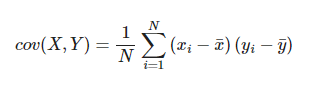
Recuerda la fórmula de la varianza:
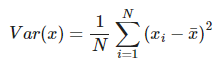
La covarianza de una variable aleatoria consigo misma es igual a la varianza:
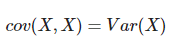
En R se calcula con la función cov(x,y):

En cambio, en el siguiente ejemplo, la covarianza falla al tratar de encontrar una relación entre dos variables por no ser lineal.

Correlación
La correlación es un valor que indica el grado de variación conjunta y lineal de dos variables aleatorias. Es la covarianza normalizada en el rango [-1, 1]. Es una forma de ignorar la variación de cada una de las variables en sí y centrarse únicamente en la relación que existe entre ambas, ya que una covarianza alta puede venir dada también porque una de las variables a estudiar tenga una varianza elevada.
Al comparar dos variables aleatorias X e Y:
- Correlación cercana a 1: para valores altos de X, tengamos mayoritariamente valores altos de Y.
- Correlación cercana a -1: para valores altos de X, tengamos mayoritariamente valores bajos de Y.
- Correlación cercana a 0: para valores altos de X, los valores de Y pueden ser altos o bajos por igual.
La función de correlación de Pearson es:
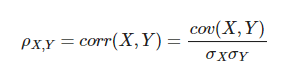
Al igual que con la covarianza, se puede calcular una matriz de correlación. Se utiliza para ver de forma sencilla cuál es la relación entre varias variables.
En una matriz de correlación la diagonal será siempre 1 (la correlación de una variable consigo misma es 1) y el valor de la celda ij vendrá dado por la correlación de la variable i con j.
En R se calcula con la función cor(x,y):

Regresión lineal
Esta es una de las relaciones entre variables en estadística Big Data y es un modelo matemático usado para aproximar la relación de dependencia entre una variable dependiente Y, la variables independiente X y un término aleatorio ε. Este modelo puede expresarse como:
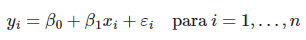
Teorema de Bayes
El teorema de Bayes describe la probabilidad de un evento basado en conocimientos previos que puede estar relacionado con el evento. Su fórmula es bastante simple:
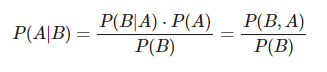
Donde A y B son nuestras variables aleatorias y P(B) ≠ 0:
- P(A|B) es la probabilidad condicional del evento A, sabiendo que ha ocurrido B.
- P(B|A) es la probabilidad condicional del evento B, sabiendo que ha ocurrido A.
- P(A) y P(B) es la probabilidad de observar A y B de forma independiente. Se conoce como la probabilidad marginal.
- P(B,A) o P(B∩A): es la probabilidad de que ambos eventos A y B ocurran a la vez.
Si son sucesos independientes P(B,A)=P(B)·P(A).
Si son sucesos dependientes P(B,A)=P(B|A)·P(A).
Por medio de este post te has familiarizado con cuáles son las relaciones entre variables en estadística Big Data y cómo se comporta cada una de ellas para el manejo de los macrodatos. Sin embargo, todavía falta mucho más por aprender dentro del ámbito de la estadística Big Data.
Es por esto que nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning es ideal para que avances con tu formación. Con él, podrás contar con una serie de módulos que te pondrán en contexto con los desarrolladores y herramientas más importantes para el procesamiento de los macrodatos, como Machine Learning, Spark & Scala, Tableau, Hadoop, etc. Todo ello de forma tanto teórica como práctica y con el acompañamiento de grandes profesionales y expertos en el universo del Big Data. ¿A qué esperas para empezar?











