¿Qué es la matemática para Machine Learning y por qué es importante?

La matemática para Machine Learning es el conjunto de bases que te permite entender cómo funcionan los modelos por dentro, no solo “usarlos”. Incluye álgebra lineal (vectores y matrices), cálculo (derivadas y gradientes), probabilidad y estadística (incertidumbre y evaluación) y optimización (cómo se entrena un modelo). Es importante porque casi todo en ML se reduce a representar datos como matrices, definir una función de error y minimizarla. Si dominas lo básico, puedes depurar mejor, elegir modelos con criterio, evitar errores comunes (como sobreajuste) y entender por qué un modelo mejora o empeora al ajustar parámetros.

¿Qué temas de álgebra lineal necesito para Machine Learning?

Lo esencial es trabajar cómodo con vectores y matrices: suma, multiplicación, transpuesta y nociones de dimensiones. Debes entender producto punto, norma (distancia), proyecciones y conceptos como independencia lineal y base, porque aparecen en reducción de dimensionalidad y representación de datos. También es muy útil tener intuición de eigenvalores/eigenvectores y descomposiciones como SVD, porque conectan directamente con PCA, embeddings y compresión de información. No necesitas demostrar teoremas avanzados, pero sí saber interpretar qué significa “multiplicar una matriz por un vector” y cómo eso transforma los datos.

¿Qué cálculo debo aprender para entrenar modelos de Machine Learning?

Debes dominar derivadas y su intuición: cómo cambia una función cuando cambias una variable. Luego pasar a derivadas parciales y gradiente, porque en ML optimizas funciones de pérdida con muchas variables (pesos). La regla de la cadena es clave, ya que es la base del backpropagation en redes neuronales. También conviene entender nociones de convexidad y curvatura (idea de Hessiano) para saber cuándo un problema es más “fácil” de optimizar. Con esto puedes comprender por qué existe el descenso por gradiente, qué hace el learning rate y por qué una función como la cross-entropy es adecuada en clasificación.

¿Qué probabilidad y estadística necesito para Machine Learning?

Necesitas probabilidad para modelar incertidumbre: variables aleatorias, distribuciones comunes (Bernoulli, Binomial, Normal), probabilidad condicional e intuición de Bayes. En estadística, lo más importante es entender media, varianza, covarianza, correlación y cómo se estima algo a partir de datos (estimadores). También debes comprender conceptos prácticos como sesgo-varianza, overfitting, validación cruzada y por qué una métrica puede engañarte si no evalúas bien. No hace falta profundizar en pruebas de hipótesis como en investigación académica, pero sí tener criterio para interpretar resultados y no sacar conclusiones erróneas con pocas muestras o datos ruidosos.

Ruta de Matemática para Machine Learning 2026

Ruta de Matemática para Machine Learning

Cuando empecé mi camino en machine learning, lo que más me costó fue entender las matemáticas subyacentes. No era solo cuestión de programar; sin una base matemática sólida, los algoritmos eran una caja negra incomprensible. Por eso quiero compartir contigo una ruta de matemáticas para machine learning que me hubiera facilitado mucho las cosas: clara, práctica y profunda, pero accesible para quienes comienzan sin perder rigurosidad.

¿Qué encontrarás en este post?

Por qué una ruta de matemáticas es clave para machine learning

El machine learning se apoya en conceptos matemáticos fundamentales para representar datos, optimizar modelos y evaluar resultados. Sin esta base, pierdes la capacidad de adaptar, mejorar o entender por qué un modelo se comporta bien o mal. Lo más común es subestimar la dificultad y sumergirse solo en la programación, pero la verdadera maestría llega cuando entiendes la matemática.

Analizando los recursos más reconocidos para aprender matemáticas en machine learning

He revisado las tres fuentes más valoradas en Google para esta temática:

Kaggle Learn – Mathematics for Machine Learning: Excelente para comenzar a practicar rápidamente con ejemplos en Python. Su enfoque práctico es inmejorable, sin embargo, la profundidad teórica es limitada para avanzar a temas complejos.
Libro Mathematics for Machine Learning, Cambridge University Press: Un clásico riguroso que cubre álgebra lineal, cálculo y probabilidad con fundamentos sólidos, pero puede ser denso para novatos o quienes buscan aplicaciones inmediatas.
Artículo en Towards Data Science Mathematics you need to learn Machine Learning: Muy claro y directo, ofrece un panorama rápido de lo esencial. No obstante, carece de ejemplos aplicados y no profundiza en la optimización, pieza clave para la mayoría de algoritmos.

¿Qué me faltó en esos contenidos? Personalmente, echo en falta una guía que:

Integre ejemplos prácticos reales y ejercicios para ensayar la teoría.
Contextualice cada bloque matemático con su importancia directa en machine learning.
Expanda la ruta incluyendo optimización convexa y técnicas para manejar incertidumbre avanzada.
Proponga recursos progresivos, con una estructura para distintos niveles y estilos de aprendizaje.

Por eso, con base en esa revisión y mi experiencia profesional en desarrollo e investigación, te propongo esta ruta optimizada.

Mi ruta recomendada de matemáticas para machine learning: paso a paso con experiencia real

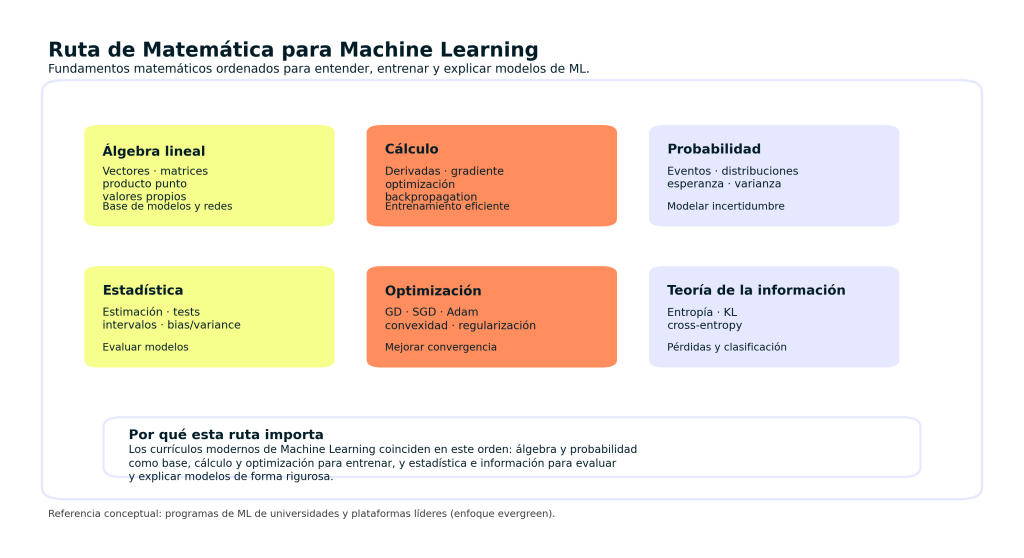
1. Álgebra lineal: el lenguaje del machine learning

Conceptos imprescindibles: vectores, matrices, sistemas lineales, espacios vectoriales, producto escalar y matriz, descomposición en valores singulares. Yo empecé con ejercicios bajos nivel y poco a poco usé Python para manipular matrices, entender transformaciones y visualizar vectores en 2D/3D.

¿Por qué imprescindible? Porque los datos se representan como matrices y vectores, y muchas técnicas se reducen a operaciones algebraicas: desde regresión lineal hasta redes neuronales. Sin este entendimiento, no puedes ni siquiera armar un pipeline correcto.

Recursos prácticos: libros como Linear Algebra and Its Applications de David Lay y plataformas como Khan Academy con ejercicios interactivos.

2. Cálculo diferencial e integral: optimizando tu inteligencia artificial

Conceptos clave: derivadas parciales y totales, gradientes, regla de la cadena, integrales, límites, funciones multivariables. Al principio, los gradientes y el descenso por gradiente me confundieron, pero al aplicarlos en código comprendí cómo se ajustan los pesos en redes neuronales.

¿Por qué es crucial? El entrenamiento de modelos es un problema de optimización en el que buscas minimizar una función por ejemplo, el error. El cálculo te da las herramientas para encontrar estos mínimos de forma eficiente.

Recurso destacado: el curso de cálculo de MIT OpenCourseWare, que combina teoría y ejercicios prácticos.

3. Probabilidad y estadística: darle sentido a la incertidumbre

Conceptos esenciales: variable aleatoria, distribuciones, normal, binomial, esperanza, varianza, teoremas fundamentales y, especialmente, el teorema de Bayes. Aquí la práctica con conjuntos de datos reales y simulaciones me ayudó a intuir por qué algunos modelos subestiman la incertidumbre.

Importancia: el machine learning es inherentemente probabilístico. Para clasificar, predecir o tomar decisiones con datos imperfectos, necesitas medir y manejar la incertidumbre.

Recurso útil: Think Stats de Allen B. Downey con ejemplos computacionales en Python.

4. Optimización convexa: la clave para entender la convergencia y estabilidad

Conceptos básicos: funciones convexas, conjuntos convexos, problemas de optimización, condiciones de optimalidad de Karush-Kuhn-Tucker. Al principio, puede sonar abstruso; pero cuando implementé algoritmos clásicos como máquinas de soporte vectorial, vi cómo estos principios garantizan que las soluciones sean estables y óptimas.

¿Por qué agregar esta etapa? Porque la mayoría de algoritmos de machine learning dependen de resolver problemas de optimización convexa. Entender este fundamento te prepara para el diseño de modelos avanzados y te evita caer en errores comunes.

Libro recomendado: Convex Optimization de Boyd y Vandenberghe.

Recursos adicionales y cómo maximizar tu aprendizaje

En adicional a los recursos mencionados, te recomiendo:

Practicar con datasets reales en Kaggle para conectar matemáticas con código.
Usar notebooks de Jupyter para visualizar el impacto de cada concepto por ejemplo, mostrando la evolución del gradiente.
Tomar cursos en plataformas como Coursera y edX que combinan teoría y práctica.
Participar en comunidades, foros y grupos de estudio para resolver dudas y compartir experiencias.

Mi consejo personal: No subestimes la importancia de avanzar paso a paso. Una vez dominado álgebra lineal, el cálculo se vuelve más intuitivo. La estadística es más digerible cuando ya entiendes cómo se usan los vectores y funciones. Y solo con todo esto en conjunto podrás entender optimización convexa.

Experiencia real: aplicando esta ruta en proyectos

En uno de mis primeros proyectos en investigación, debía implementar un clasificador para detectar anomalías en datos médicos. Al principio usé librerías sin entender los fundamentos; el modelo era inestable y difícil de mejorar. Cuando volví a estudiar álgebra lineal y optimización, logré ajustar el algoritmo y explicar sus resultados al equipo clínico con confianza. Esa experiencia confirmó que la ruta de matemáticas para machine learning no es opcional, sino esencial para avanzar.

Conclusión: tu camino para dominar la matemática del machine learning

Si quieres ir más allá de copiar código o seguir gurús, seguir una ruta estructurada y profunda como la que propongo te hará un profesional capaz y seguro. Recuerda: álgebra lineal, cálculo, probabilidad y optimización son las bases. Acompáñalas con práctica, ejemplos y recursos adecuados a tu ritmo.

Para profundizar en machine learning desde cero y con énfasis en fundamentos matemáticos y prácticos, te invito a conocer el Bootcamp Big Data, Data Science, ML & IA Full Stack. Allí transformarás tu vida profesional con experiencia real guiada por expertos.