La similitud entre vectores, también denominada cosine similarity o similitud del coseno, es una medida que se utiliza para calcular la similitud entre dos o más vectores. La similitud del coseno es el coseno del ángulo entre vectores. Los vectores suelen ser distintos a cero y están dentro de un espacio de producto escalar.
En términos matemáticos, la similitud del coseno se describe como la división entre el producto escalar de los vectores y el producto de las normas euclidianas o la magnitud de cada vector.
Similitud entre vectores
La similitud entre vectores o cosine similarly está dada por la fórmula matemática del producto escalar:
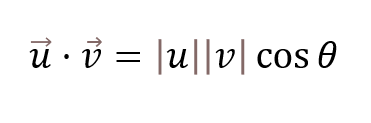
Esta fórmula no es más que esto:
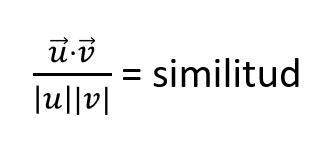
Con esta ecuación sobre la similitud entre vectores o cosine similarity vectors podemos calcular cómo de similares son dos vectores. Si nos fijamos, lo único que ha cambiado es que los términos |u| |v| se han movido para ser los divisores de la ecuación, mientras que el coseno de θ ha pasado a ser ese término nuevo que estamos introduciendo, que es la similitud.
La parte de arriba de nuestra ecuación representa el producto escalar y la parte de abajo es el producto del módulo de los vectores.
¿Qué es el módulo de un vector?
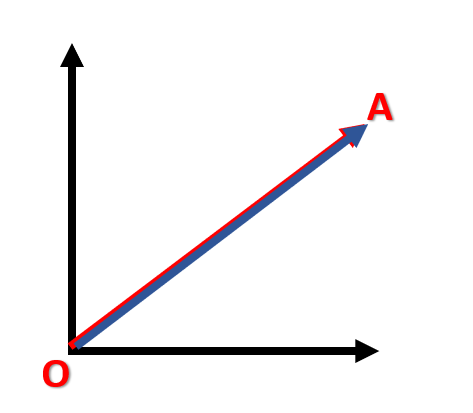
Antes de seguir, aclaremos un poco el concepto de módulo. El módulo no es más que la longitud que tiene el vector. En caso de que tengamos un eje de coordenadas de dos dimensiones que va de O a A, el módulo sería la longitud entre O y A y se denotaría con |AO|.
Pese a llamarse módulo, lo único que indica es la longitud del vector; se le denomina módulo porque puede utilizarse no solo con uno o dos componentes, sino con muchísimos más, ya sea en dos o en tres dimensiones.
Aquí estamos calculando el módulo del vector l:
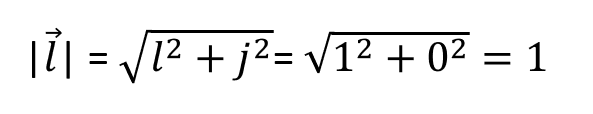
Y el módulo del vector j:
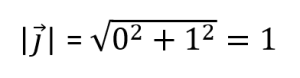
Nos dice que la longitud del vector l es 1, al igual que la longitud del vector j. Eso tiene sentido, porque los ejes unitarios, como su nombre indica, tienen unidad 1 y, por tanto, tienen longitud 1. ¿Y cómo calculamos esa longitud? Pues la calculamos con la ecuación de l, donde simplemente sumamos el cuadrado de los componentes del vector y eso nos va a dar el resultado del módulo.
De este modo, siempre el resultado del producto del módulo de un vector va a ser un número, al igual que sucede con el producto escalar, donde el resultado siempre va a ser un escalar.
Más acerca de la similitud entre vectores
La similitud entre vectores o cosine-similarity es una técnica muy usada y, por tanto, se puede encontrar fácilmente en librerías como Matlab, Scikit learn y TensorFlow.
La similitud entre vectores es muy beneficiosa porque, incluso cuando los vectores tienen una distancia euclidiana muy grande, estos podrían tener un ángulo pequeño entre ellos. Cuanto menor es el ángulo, mayor es la similitud entre vectores.
La similitud entre vectores es un valor que va a estar limitado por un rango restringido de 0 y 1.
Supongamos que dos vectores tienen un ángulo de 90°. En ese caso específico, la similitud entre vectores tendrá un valor de 0, lo cual significaría que los vectores son ortogonales o, dicho de otro modo, perpendiculares entre sí.
La similitud entre vectores tiene muchos campos de aplicación, entre ellos está la validación de documentos para saber cómo de similares son.
Asimismo, se puede utilizar en pose matching, donde lo que se busca es establecer la similitud entre dos poses en una imagen.
Ejemplo de similitud de coseno
Para este ejemplo de similitud de coseno supongamos que tenemos dos imágenes.
Imagen 1: tenemos una matriz que tiene:
[236 2 32 56
20 72 31 8] píxeles por píxeles
Imagen 2: tenemos otra matriz con valores distintos:
[52 2 20 25
72 241 23 7] píxeles por píxeles
Estas imágenes las podemos convertir en vectores de la siguiente forma, por medio de un ejercicio o ejemplo de similitud de coseno:
En la primera fila tenemos [236 2 32 56], que concatenamos inmediatamente a la segunda fila [20 72 31 8], con lo cual quedaría [236 2 32 56 20 72 31 8], y así sucesivamente, si tuviéramos más filas las concatenaríamos de manera seguida para formar un vector.
El vector resultante tendría 256 x 256: R256 x 256. En el primer caso, es decir, en el caso de la matriz, ese 256×256 se está refiriendo al número de filas y columnas, respectivamente. En el segundo caso, ese número hace referencia o, más bien, se traduce como una multiplicación, porque estamos concatenando uno tras otro.
Con la segunda imagen hacemos exactamente lo mismo que con la anterior, por lo que nos quedaría: [52 2 20 25 72 241 23 7].
Tendríamos dos vectores con la misma cantidad de componentes y esto nos permitiría calcular la similitud entre las dos imágenes.
Entonces, esto nos permite ver un ejemplo de similitud de coseno en donde transformamos de matriz a vector.
Este modo de transformación de las imágenes se utiliza mucho en redes convolucionales, concatenándose los píxeles de una imagen tras otra.
Como podemos observar, este tipo de temáticas se emplean mucho en el campo del machine learning, especialmente en deep learning y redes neuronales.
Ahora que hemos visto cómo funciona la similitud entre vectores, podemos seguir aprendiendo sobre Big Data, una de las disciplinas más demandadas de la actualidad y mejor pagas. Para ello tenemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva e íntegra en la que podrás adquirir todos los conocimientos teóricos y prácticos necesarios para incursionar en el mercado laboral de manera rápida y eficiente.
¡Anímate a seguir cambiando tu futuro y convertirte en un data scientist de gran éxito y solicita más información ahora!







