¿Alguna vez has pensado cuál es la relación que existe entre los sistemas de ecuaciones y combinaciones lineales? En este artículo te contamos un poco acerca de ello.

¿Recuerdas cómo funcionan las combinaciones lineales entre vectores? Pues bien, ahora vamos a intentar resolver un sistema de ecuaciones usando todo lo que sabemos hasta el momento sobre matrices para poder calcular la combinación lineal de estos vectores.

Sistemas de ecuaciones y combinaciones lineales: ejercicio

Veamos un ejercicio sobre sistemas de ecuaciones y combinaciones lineales para entender mejor la relación entre ellos.

Escribe cada uno de los siguientes vectores (v₁, v₂, v₃) como combinación lineal de A.

v₁ = [3, 0, 0] v₂ = [0, 2, 0] v₃ = [0, 0, 1]

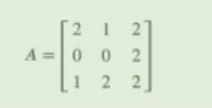
Recordemos que la transformación lineal la podemos escribir como A . X = B.

Entonces, el ejercicio sobre sistemas de ecuaciones y combinaciones lineales consiste en resolver el siguiente sistema de ecuaciones:

A . X = B

X = A^-1 . B

Donde A viene dado por:

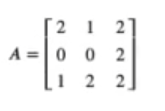
Y donde B está conformado por los vectores v₁, v₂, v₃:

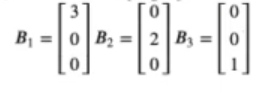
Recordemos que lo único que queremos en estos sistemas es sacar la X de ambas ecuaciones. La inversa de la matriz nos deshacía la transformación, de modo que lo que pretendemos hacer es, teniendo en cuenta la matriz de transformación y el vector resultante (en este caso son tres: v1 = [3, 0, 0] v2 = [0, 2, 0] v3 = [0, 0, 1]), calcular el vector que ha generado esta transformación.

Por tanto, vamos a resolver este sistema de ecuaciones X = A^-1 . B, primero para B₁ = [3, 0, 0].

Lo primero que haremos será escribir la matriz A por medio del comando np.array. Para resolverla, solo tenemos que calcular la inversa:

#Sistemas de ecuaciones y combinaciones lineales
A = np.array ([[2,  1,  2],
                         [0,  0,  2],
                         [1,  2,  2]])

inv_A = np.linalg.inv (A)
print (inv_A)

[[ 0.66666667 -0.33333333 -0.33333333]

[ -0.33333333 -0.33333333 0.66666667]

[ 0. 0.5 0. ]]

Veamos cómo hacerlo. El primer caso B₁. B₁ viene dado por [3 0 0] y lo único que queremos es resolver el producto matricial de la inversa de A . B. Eso nos dará X, que es el vector original, antes de la transformación.

#Sistemas de ecuaciones y combinaciones lineales
#B1

B1 = np.array ([[3],
                           [0],
                           [0]])

X1 = np.dot (inv_A, B1)
print (X1)

[[ 2. ]

[ -1. ]

[ 0. ]]

Hacemos lo mismo para B₂ = [0, 2, 0]

#Sistemas de ecuaciones y combinaciones lineales
#B2

B2 = np.array ([[0],
                           [2],
                           [0]])

X2 = np.dot (inv_A, B2)
print (X2)

[[ -0.66666667 ]

[ -0.66666667 ]

[ 1. ]]

Y para B₃ = [0, 0, 1]

#Sistemas de ecuaciones y combinaciones lineales
#B3

B3 = np.array ([[0],
                           [0],
                           [1]])

X3 = np.dot (inv_A, B3)
print (X3)

[[ -0.33333333 ]

[ -0.66666667 ]

[ 0. ]]

Si te interesa acceder a una de las disciplinas más demandadas y mejor pagadas de todo el mercado laboral en pocos meses, puedes hacerlo gracias al Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. Esta es una formación íntegra y de alta intensidad en la que adquirirás todos los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar más información y anímate a cambiar tu futuro!