El sobreajuste en estadística Big Data es uno de los factores que podrás encontrar en tu procesamiento de datos durante el estudio estadístico. Este se conoce como uno de los errores más comunes al utilizar determinados modelos que no compaginan con los datos que te encuentras procesando, por ello, caer en este es muy frecuente.
Por este motivo, en este post, te explicamos qué es el sobreajuste en estadística Big Data por medio de ejemplos que lo clarifican.
¿Qué es el sobreajuste en estadística Big Data?
El sobreajuste en estadística Big Data (overfitting) ocurre en los modelos que tienen un grado polinómico tan alto que empiezan a seguir al ruido, de manera que se sobreajustan demasiado a los datos, perdiendo una visión más general de los datos y proporcionando predicciones erradas.
En este caso, en lugar de estar aprendiendo la relación básica entre dos variables, estarías aprendiendo los errores, ya que el modelo empleado intenta integrar los errores para dar una respuesta más exacta. El problema es que al coger otra vez las variables similares los errores cambian, por lo que lo aprendido con los errores anteriores ya no sirve y el modelo sería erróneo.
El sobreajuste en estadística Big Data enseña que no hay que perderse demasiado en los detalles y las pequeñas variaciones de una variable, dado que la esencia del modelo se basa en encontrar una predicción que funcione para la mayoría de los casos. No se pretende que funcione solo para los datos que se están viendo ahora mismo, sino también para los datos futuros que te llegarán.
Por ejemplo
Ahora, te compartimos un ejemplo que clarifica cómo se presenta este sobreajuste en cierto modelo:
modelOverfit <- lm(Y~poly(x,27)) summary(modelOverfit)
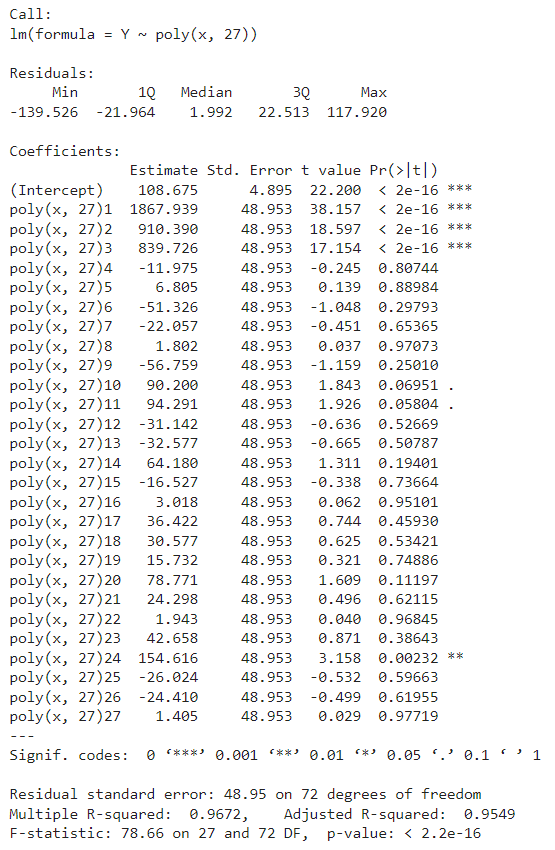
plot(X[,2],Y,pch='*') xp<-seq(-10,10,by=0.1) yp<-predict(modelOverfit,data.frame(x=xp)) lines(xp,yp,col="blue") lines(xp,predict(modelPoly3,data.frame(x=xp)),col="red")
paste("Polinomio grado 27: Rsquared:",summary(modelOverfit)$r.squared)
paste("Polinomio grado 27: Residual standard error",sqrt(sum(summary(modelOverfit)$residuals^2)/(length(summary(modelOverfit)$residuals)-25)))
paste("Polinomio grado 3: Rsquared:",summary(modelPoly3)$r.squared)
paste("Polinomio grado 3: Residual standard error",sqrt(sum(summary(modelPoly3)$residuals^2)/(length(summary(modelPoly3)$residuals)-4)))
‘Polinomio grado 27: Rsquared: 0.967209419375986’
‘Polinomio grado 27: Residual standard error 47.9644017918624’
‘Polinomio grado 3: Rsquared: 0.954608949821556’
‘Polinomio grado 3: Residual standard error 49.8797892133702’
¿Cómo encontrar el mejor modelo?
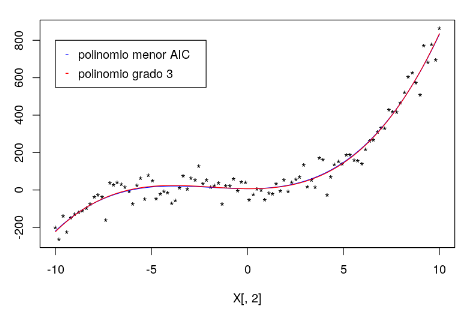
Podrás usar el p-valor de los coeficientes o buscar entre todos los modelos el de menor AIC.
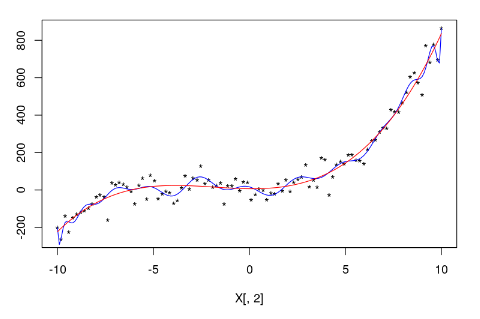
El criterio de información de Akaike (AIC) es un estimador de la calidad relativa del modelo que tiene en cuenta su complejidad.
A medida que se aumenta el número de parámetros de entrada o de grados de un polinomio, el valor del error cuadrático medio va a ser mejor porque el error cuadrático medio disminuye. El AIC penaliza los modelos complejos en favor del los sencillos para evitar el sobreajuste, como puedes ver a continuación:
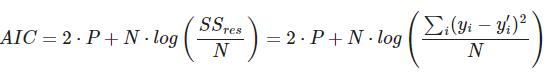
Aquí, P es el número de variables que se utilizan en el modelo y N el número de muestras. Cuanto menor sea el valor del AIC, mejor será el modelo.
Continua aprendiendo sobre el Big Data
En este post, te hemos expuesto cómo funciona el sobreajuste en estadística Big Data por medio de ejemplos prácticos que te aconsejamos llevar al método de ensayo y error, de manera que logres comprenderlo en profundidad para adecuar sus procesos a tu análisis de macrodatos.
Ahora que conoces y comprendes el sobreajuste en estadística Big Data, desde KeepCoding te aconsejamos que continúes aprendiendo sobre herramientas y lenguajes del Big Data. Con el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, desde la fase de prebootcamp ya podrás afianzar tu base de SQL, Python/Django y el despliegue de aplicaciones en servidor, Docker, Javascript y Linux desde cero. ¿A qué esperas para convertirte en todo un experto? ¡Apúntate!











