Los SVR (Support Vector Regression), también conocidos como SVM en regresión (Support Vector Machines), son un método que puede utilizarse en regresión (aunque inicialmente el SVM se creó para algoritmos de aprendizaje en clasificación).
Su traducción es máquinas de vectores de soporte y se utilizan para resolver problemas de clasificación y regresión con conjuntos de datos o datasets.
El SVM en regresión acepta los mismos kernels que SVC, funciona sobre la librería libsvm y controla la penalización de los errores en épsilon (en scikit learn) o parámetro ϵ.
En este post, te explicaremos cómo funcionan los SVM en regresión.
Intuición de un SVM en regresión
Lo que se pretende con el SVM en regresión es buscar el hiperplano que mejor se ajuste a los datos y permita una tolerancia a los errores. En otras palabras, es una regresión lineal con restricciones.
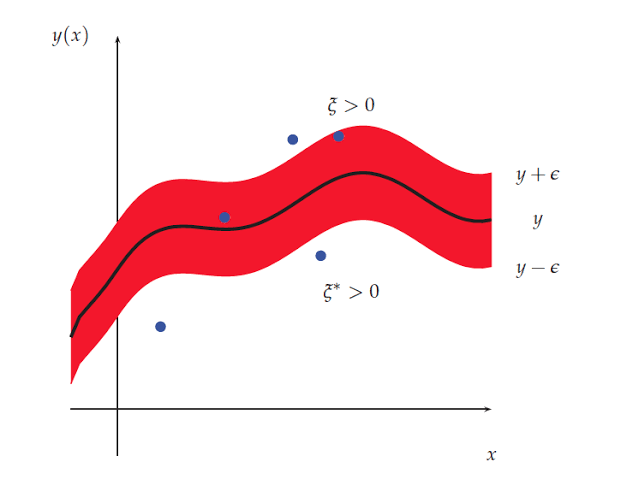
La diferencia intuitiva que hay entre un SVR y un SVC es que en clasificación lo que pretendemos es que las muestras queden fuera del margen, mientras que en regresión lo que queremos es que queden dentro del margen, porque lo que intentamos hacer es que estas se ajusten a los datos.
Conceptos a tener en cuenta para formular un SVM en regresión
Existen algunos conceptos que debemos tener en cuenta en el momento de trabajar con SVR o SVM en regresión. Entre ellos están:
Hiperplano
El hiperplano es lo que separa dos espacios pertenecientes a las clases. El SVM siempre va a buscar que un hiperplano separe lo más óptimamente posible los puntos de una clase en relación con otra; estos podrían haberse proyectado previamente en un espacio de dimensionalidad superior.
Cuando se tiene un conjunto de entrenamiento, se busca que el hiperplano encuentre la función f : Rh → ± 1f : Rh → ± 1 que separe los datos en dos clases y que haga pronósticos acertados de las nuevas muestras que ingresen en el conjunto de pruebas o validación.
Kernel
Un kernel o núcleo es un conjunto de algoritmos y funciones matemáticas que se utilizan en SVM y que permiten realizar operaciones algebraicas en Rh de manera eficiente.
Existen diferentes tipos de kernel:
- Kernel lineal: K (xi, xj) = xiT ∗ xj
- Kernel polinomial: K (xi, xj) = (p + ΥxiT ∗ xj) d, Υ > 0
- Kernel gaussiano RBF: K (xi, xj) = exp (−Υ ||xi − xj|| 2), Υ > 0
Formulación de SVM en regresión
Queremos que nuestra solución sea de la forma y = ƒ (x) = ωTx + ω0 y permitir errores dentro del «margen»: [y – ∈, y + ∈], así que el funcional a minimizar es similar al problema de clasificación.
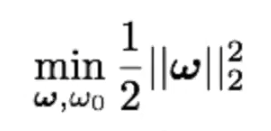
s.to y(i) – (ωTx(i) + ω0) ≤ ∈
-y(i) + (ωTx(i) + ω0) ≤ ∈
Pero cabe hacernos una pregunta: ¿qué hacemos con las muestras que caen fuera del margen?
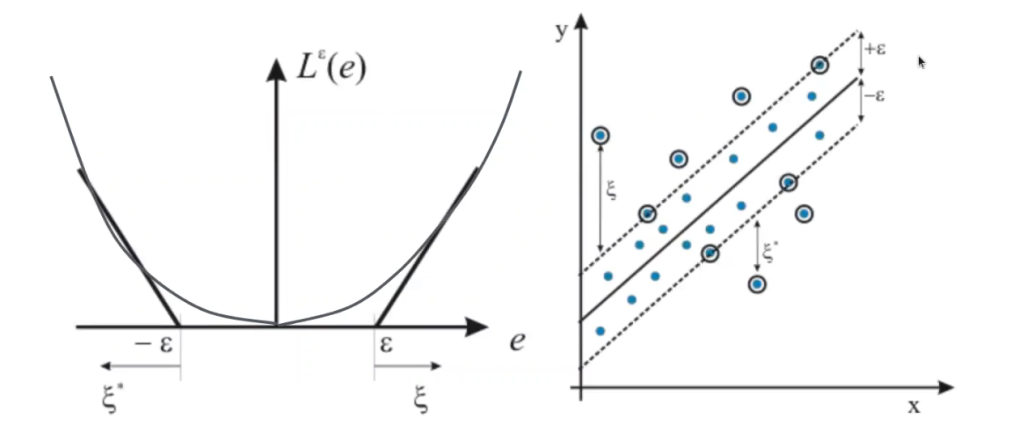
Lo que podemos hacer con estas muestras es penalizarlas. Esto significa que los SVR o SVM en regresión son exactamente lo mismo que los SVC o SVM en clasificación, con una pequeña pero sustancial diferencia: el procedimiento SVR es inverso al de SVC, ya que lo que buscamos es que todo quede dentro del margen y que se puedan ajustar los datos en regresión, en vez de que se puedan separar para hacer clasificación.
Veamos, pues, una regresión lineal con función de coste e – insensible:
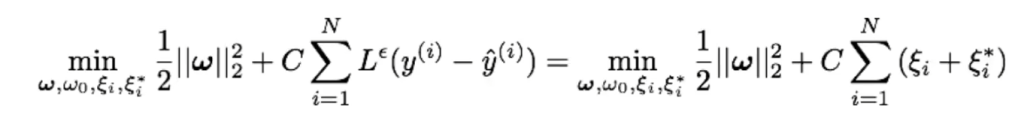
Esta regresión está sujeta a ciertas restricciones:
- y(i) – (ωTx(i) + ω0) ≤ ∈ + ζi
- -y(i) + (ωTx(i) + ω0) ≤ ∈ + ζi*
- ζi, ζi ≥ 0
Coeficientes:
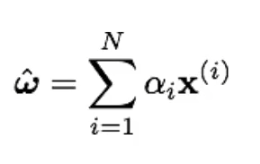
Así pues, esta es una combinación lineal de las muestras de entrenamiento.
Regresión:
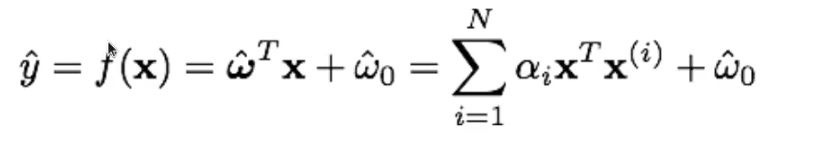
Se hace un producto escalar entre las muestras de entrenamiento y la muestra sobre la que queremos realizar la predicción.
¿Qué sigue?
Si te gustaría seguir aprendiendo, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos necesarios para seguir construyendo un brillante futuro como data scientist.
El Big Data es una de las disciplinas más demandadas y mejor pagadas en la actualidad y con una amplia gama de subtemas que puedes estudiar y aprender. No esperes más, ¡sigue forjando tu camino hacia el éxito y solicita más información ahora!











