En este artículo realizaremos un test A/B con GLM, donde simularemos que tenemos dos webs, una de control y una nueva, y se evaluará el nivel de éxito en cada una de ellas.
Desarrollo del test A/B con GLM
na_t <- 1000
na_s <- 197
nb_t <- 1000
nb_s <- 230
m <- matrix (c (na_s, na_t, nb_s, nb_t), byrow = T, nrow = 2,
dimnames = list (c ("control", "nuevo"), c ("exitos", "intentos")))| éxitos | intentos | |
| control | 197 | 1000 |
| nueva | 230 | 1000 |
Lo que nos está diciendo la tabla es que, en la web de control, de 1000 ha habido 197 aciertos (por ejemplo, 197 compras). Además, en la web nueva, entre esos mismos 1000 intentos ha habido 230 éxitos.
Hacemos el test chisq y nos dice que el p-valor es 0.16, es decir, no podemos decir con seguridad que es mejor la web nueva que la de control. Al parecer, en la nueva tenemos un 16% más de éxito, pero se requerirían más pruebas para corroborar esta información.
chisq.test (m)
El 0.1626 que aparece aquí es el dato en bruto, es decir, con ambas web tenemos el mismo número de intentos (1000 intentos). Este valor nos está diciendo que la web nueva tiene un 16% más de probabilidad de éxito que la web de control con el test A/B con GLM.
No obstante, según el test chisq, el p-valor es muy alto y tampoco hay mucha seguridad de que la nueva sea mejor.
df = data.frame (m)
df$type <- factor (rownames (df))
df
dfsexitos [2] / dfsexitos [1]Vamos a utilizar la regresión logística para resolver este ejercicio.
Resolución de Test A/B con GLM (binomial)
Este ejercicio se podría resolver perfectamente con un test de Bayes, pero ahora veremos una solución muy rápida que nos permite hacer cálculos en segundos para poder resolver el ejercicio de las web del test A/B con GLM. Esta solución tiene que ver con la distribución binomial.
Utilizaremos el cbind éxitos – intentos-éxitos (o sea fracasos):
model <- glm (cbind (exitos, intentos - exitos) type, family = binomial, data = df)
summary (model)
exp (model$coef [2])
exp (confint (model))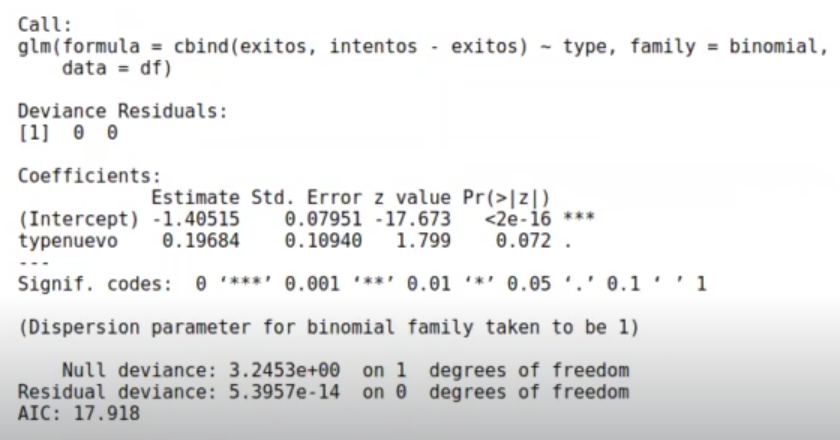
Number of Fisher Scoring iterations: 2
typenuevo: 1.21754894851309
Waiting for profiling to be done...
Tenemos que el exponente del coeficiente es 1.21754894851309. Esto lo que nos está diciendo es cuánto mejor es la web nueva respecto a la web de control.
En el ejercicio del test A/B con GLM, el número de veces, el coeficiente 2, es la razón de momios, el cómo afecta el tener un tipo nuevo a no tenerlo.
¿Cómo afecta? Pues debemos fijarnos en el typenuevo, que es el exponente; en este caso es 0.19684. El exponente está refiriéndose a cuánto incrementa la razón de momios en el caso de tener el tipo nuevo de web a no tenerlo.
El typenuevo nos está diciendo que aumenta un 21%, es decir, la web mejora este porcentaje.
Ahora, veamos los márgenes de confianza:
| 2.5 % | 97.5 % | |
| (Intercept) | 0.2093957 | 0.2860216 |
| typenuevo | 0.9828441 | 1.5067350 |
Siguiendo con el ejercicio del test A/B con GLM, los márgenes de confianza lo que nos están diciendo es que con la web nueva puede suceder que empeora un 98% o que mejora un 50%. Básicamente esto significa que la web nueva tiene una posibilidad de fracaso o de empeorar ese 2% restante del 98%, pero que tiene una posibilidad de éxito del 50%.
Con este test binomial vemos que el p-valor es más bajo y, sobre todo, los coeficientes nos están explicando que, si bien puede que la web de tipo nuevo sea peor, si eso resulta ser cierto, será tan solo un 2% peor que la web de control; empero, puede que sea mucho mejor, incluso hasta un 50%.
El exponencial de la suma de los coeficientes es equivalente a la razón de momios de la posibilidad de éxito respecto a la posibilidad de fracaso para la web nueva:
exp (-1.40515 + 0.19684) = razón monomios éxito / fracaso para web nuevaY el exponencial de -1.40515 equivale a la posibilidad de éxito de la web nueva.
exp (0.19684) es la mejora de usar la web nueva respecto a la vieja. Es decir, mejorará un 21% de media, con intervalos de confianza:
exp (confint (model))| 2.5% | 97.5% | |
| (Intercept) | 0.2097957 | 0.2860216 |
| typenuevo | 0.9828441 | 1.5094350 |
¿Qué sigue?
El test A/B con GLM mezclado con un modelo de regresión logística puede ser un tema complicado; no obstante, no debes sentirte agobiado, porque tenemos la solución para ti. Por medio de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp aprenderás todas estas temáticas y otras muchas relacionadas.
Durante 8 meses estarás acompañado de los mejores instructores para que sigas forjando tus conocimientos y construyendo tu camino hacia el éxito. Y cuando termines, recibirás asesoramiento de por vida para entrar y crecer en el mercado laboral. ¡Anímate y solicita más información!











