¿Sabés cuáles son los tipos de distribuciones en estadística Big Data? Los tipos de distribuciones en estadística forman parte de las funciones de probabilidad con los que podrás contar para llevar a cabo un estudio del tipo estadístico en los macrodatos, de manera que se extraiga el conocimiento de estos grandes volúmenes de datos a través de estrategias funcionales y efectivas. En este post, profundizamos en ellos.
¿Cuáles son los tipos de distribuciones en estadística?
Los tipos de distribuciones en estadística constituyen componentes esenciales de las funciones de probabilidad que surgen con mayor frecuencia durante la realización de investigaciones estadísticas.
A modo de resumen, estos son los tipos distribuciones en estadística Big Data:
- Distribución uniforme: es continua y todos los valores tienen la misma probabilidad.
- Distribución Bernoulli: se trata de una distribución discreta con dos posibles resultados. Por ejemplo, lanzar una moneda al aire.
- Distribución exponencial: es una distribución continua que representa el tiempo medio entre eventos de una distribución de Bernoulli.
- Distribución binomial: es una distribución discreta y se considera una generalización de la distribución Bernoulli. Por ejemplo, lanzar varias monedas al aire.
- Distribución de Poisson: se trata de una distribución discreta que generaliza la distribución binomial cuando hay un número infinito de eventos con una probabilidad muy baja.
- Distribución gaussiana: es continua y muy utilizada; cualquier combinación de variables aleatorias tiende a seguir una distribución gaussiana.
- Distribución chi cuadrado: es una distribución continua y se obtiene al cuadrar una distribución gaussiana.
Distribuciones continuas
Entre los tipos de distribución de probabilidad en estadística se encuentran:
Distribución uniforme
Es una familia de funciones de probabilidad de distribuciones estadísticas donde cada elemento, dentro de cierto intervalo, tiene la misma probabilidad de aparecer.
Ejemplo: la lotería, todos los números tienen las mismas posibilidades.
Estimadores media y varianza:
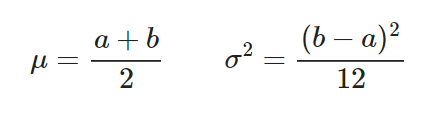
Funciones en R:
- runif(x,min=a,max=b): genera x números aleatorios.
- dunif(x,min=a,max=b): función de densidad en el punto x (likelihood).
- punif(x,min=a,max=b): probabilidad acumulada P(X<x)=p.
- qunif(p,min=a,max=b): inversa de la probabilidad acumulada P(X<x)=p.
Podrás generar una variable aleatoria que siga una distribución uniforme mediante la función runif().
Por ejemplo, para generar 10000 muestras de una distribución uniforme entre 2 y 7 basta con ejecutar en R:
set.seed(1)
myUnifVector <- runif(10000, min = 2, max = 7)
summary(myUnifVector)
length(myUnifVector)Distribución gaussiana
La distribución normal o gaussiana es posiblemente la forma de la distribución de probabilidad más utilizada. Su importancia radica en el teorema central del límite.
Su función de densidad de probabilidad es:
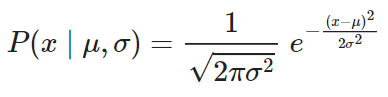
La función acumulativa de probabilidad no tiene una forma explícita:
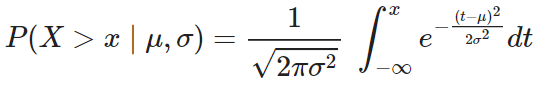
Distribución chi cuadrado
La distribución chi-cuadrado con ( k ) grados de libertad se obtiene al sumar los cuadrados de ( k ) variables aleatorias independientes que siguen una distribución normal estándar (gaussiana con media 0 y desviación estándar 1). En otras palabras, si ( Z_1, Z_2, \ldots, Z_k ) son variables aleatorias independientes con distribución normal estándar, entonces la variable ( X = Z_1^2 + Z_2^2 + \ldots + Z_k^2 ) sigue una distribución chi-cuadrado con ( k ) grados de libertad, denotada como ( X \sim \chi^2(k) ). Este concepto es esencial en estadística y se utiliza en varias pruebas y análisis de datos.
Su función de distribución es:
Distribuciones discretas
Distribución de Bernoulli
Es una distribución discreta que puede tomar dos valores uno con probabilidad y otro no. Se utiliza para describir sucesos que solo tienen dos posibles resultados, como Si/No, 1/0 o Cara/Cruz.
Ejemplo: tirar una vez una moneda al aire.
Estimadores media y varianza:
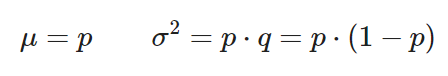
La distribución de Bernoulli es un caso especial de la distribución binomial con n=1. Podrás simular una distribución de Bernoulli a partir de una uniforme simplemente comparando si el valor supera un umbral que viene determinado por la probabilidad de la distribución binomial.
Distribución binomial
La distribución binomial es una generalización de la distribución de Bernoulli para sucesos independientes, cada uno de los cuales tiene dos posibles resultados Si/No con probabilidad .
Ejemplo: tirar al aire tres monedas y mirar cuál es la probabilidad de que en dos salga cara.
Variables que definen la distribución:
- p – probabilidad de éxito de un caso individual.
- n – número de eventos totales que se desean medir.
- k – número de eventos en los que ha salido SI.
Estimadores media y varianza:
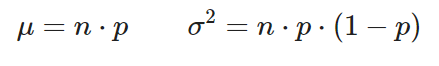
Distribución de Poisson
Tiene su origen en una distribución binomial a medida que n -> ∞ y p -> 0, manteniendo λ = n · p constante.
Esta distribución expresa la probabilidad de que un número de eventos dado ocurra en un intervalo de tiempo (o espacio) fijo si los eventos ocurren con una frecuencia constante y son independientes (no dependen de cuándo ocurrió el último evento).
Ejemplo: número de llamadas que cursa una antena de telefonía móvil en una franja horaria.
Estimadores media y varianza:
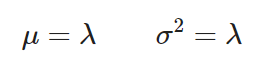
Distribución exponencial
Describe el tiempo que transcurre entre dos eventos que siguen una distribución de Poisson. Es decir, dado un proceso que produce eventos de forma continua e independiente a una tasa constante, el tiempo entre dos eventos vendrá dado por una distribución exponencial.
Ejemplo: tiempo entre dos llamadas consecutivas que llegan a una antena de telefonía móvil en una franja horaria.
Estimadores media y varianza:
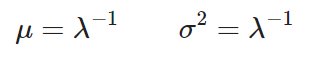
Por medio de este post, te has familiarizado con los tipos de distribuciones en estadística Big Data y cómo funciona cada una de estas alternativas para llevar a cabo un estudio estadístico de los macrodatos. Sin embargo, esta es una de las ramas más amplias del mundo del manejo Big Data, por lo que te aconsejamos continuar aprendiendo al respecto.
Para ello, desde KeepCoding te ofrecemos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning. En el desarrollo de esta formación, te encontrarás con una serie de conocimientos íntegros para llevar a cabo una gestión de la información apropiada según el interés y el planteamiento del problema establecido. ¡Anímate a cambiar tu vida y apúntate ahora mismo!
