El Deep Learning es uno de los campos más amplios para el manejo de los macrodatos; no obstante, también es una gran herramienta para el procesamiento del Big Data. En este post, te exponemos los tipos de inicialización de pesos en Deep Learning.
Tipos de inicialización de pesos en Deep Learning
Los tipos de inicialización de pesos en Deep Learning se presentan, ya que muchas de las funciones de activación necesitan métodos específicos de inicialización de pesos, para que estén dentro de unos valores y que el descenso del gradiente funcione adecuadamente.
Veamos qué es lo que pasa si empleamos diferentes funciones de activación con los tipos de inicialización de pesos en Deep Learning:
# Ejemplos de funciones de activación con tipos de inicialización de pesos en Deep Learning # Para ello, primero hacemos los imports necesarios y después definimos una # función que creará y entrenará la red, teniendo como entrada la función de # activación que queremos usar. # imports necesarios import numpy as np import matplotlib.pyplot as plt import tensorflow as tf # importamos el dataset MNIST y cargamos los datos from tensorflow.examples.tutorials.mnist import input_data mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
# definimos la función para entrenar nuestra red con los parámetros deseados de tipos de inicialización de pesos en Deep Learning def train_network_decay_fnact(activation_function, learning_rate, lr_decay, batch_size, n_epochs): # creamos los contenedores para nuestras entradas y salidas x = tf.placeholder(tf.float32, [None, 784]) # imágenes del mnist: 28*28=784 y = tf.placeholder(tf.float32, [None, 10]) # número indicando la clase 0-9 => 10 clases # ahora creamos las variables W y b para el entrenamiento W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10])) # por último, construimos el modelo pred = activation_function(tf.matmul(x, W) + b) # definimos nuestra función de pérdidas: esta vez, la cros-entropía # la verás como loss o cost: es lo mismo cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1)) # calculamos los gradientes (gradient descent) grad_W, grad_b = tf.gradients(xs=[W, b], ys=cost) # definimos las operaciones para actualizar los pesos con los gradientes calculados # e implementamos el learning rate decay new_W = W.assign(W - learning_rate * (1-lr_decay) * grad_W) new_b = b.assign(b - learning_rate * (1-lr_decay) * grad_b) # inicializamos las variables init = tf.global_variables_initializer() # para almacenar el histórico de costes costs = [] # inicializamos current_lr current_lr = learning_rate # empezamos la sesión with tf.Session() as sess: sess.run(init) # entrenamiento de nuestra red for epoch in range(n_epochs): avg_cost = 0. total_batch = int(mnist.train.num_examples/batch_size) # si en vez de actualizar los pesos para cada imagen, ¿lo hacemos # de X en X imágenes? for i in range(total_batch): batch_xs, batch_ys = mnist.train.next_batch(batch_size) # ejecutamos la optimización Wc, bc, c = sess.run([new_W, new_b ,cost], feed_dict={x: batch_xs, y: batch_ys}) # calculamos el coste teniendo en cuenta los batches que hay avg_cost += c / total_batch # actualizamos el learning_rate igual que lo hace tensorflow current_lr = current_lr * (1-lr_decay) # guardamos nuestro coste en el histórico costs.append(avg_cost) # Imprimimos las iteraciones # current_lr = learning_rate * (1-lr_decay) ** (epoch * batch_size + i) print("[{}] cost: {} lr: {}".format(epoch, avg_cost, current_lr)) print("Entrenamiento finalizado!!") # comprobamos lo que ha aprendido nuestra red correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1)) # calculamos el accuracy (precisión) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) print("Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels})) # observemos nuestra función de pérdidas con respecto a las épocas ejecutadas plt.plot(np.arange(0, n_epochs), costs) plt.title("Training Loss") plt.xlabel("Epoch #") plt.ylabel("Loss")

# cambiamos la inicialización de los pesos a 1s en vez de 0s como uno de los tipos de inicialización de pesos en Deep Learning
# definimos la función para entrenar nuestra red con los parámetros deseados
def train_network_decay_fnact_w1_b1_mse(activation_function, learning_rate, lr_decay, batch_size, n_epochs):
# creamos los contenedores para nuestras entradas y salidas
x = tf.placeholder(tf.float32, [None, 784]) # imágenes del mnist: 28*28=784
y = tf.placeholder(tf.float32, [None, 10]) # número indicando la clase 0-9 => 10 clases
# y creamos las variables W y b para el entrenamiento
W = tf.Variable(tf.ones([784, 10]))
b = tf.Variable(tf.ones([10]))
# por último, construimos el modelo
pred = activation_function(tf.matmul(x, W) + b)
# ahora, definimos nuestra función de pérdidas: esta vez, la cros-entropía
# cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(pred), reduction_indices=1))
cost = tf.reduce_mean(tf.squared_difference(pred, y))
# calculamos los gradientes (gradient descent)
grad_W, grad_b = tf.gradients(xs=[W, b], ys=cost)
# definimos las operaciones para actualizar los pesos con los gradientes calculados
# e implementamos el learning rate decay
new_W = W.assign(W - learning_rate * (1-lr_decay) * grad_W)
new_b = b.assign(b - learning_rate * (1-lr_decay) * grad_b)
# inicializamos las variables
init = tf.global_variables_initializer()
# para almacenar el histórico de costes
costs = []
# inicializamos current_lr
current_lr = learning_rate
# empezamos la sesión
with tf.Session() as sess:
sess.run(init)
# entrenamiento de nuestra red
for epoch in range(n_epochs):
avg_cost = 0.
total_batch = int(mnist.train.num_examples/batch_size)
# y si en vez de actualizar los pesos para cada imagen, ¿lo hacemos
# de X en X imágenes?
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# ejecutamos la optimización
Wc, bc, c = sess.run([new_W, new_b ,cost], feed_dict={x: batch_xs,
y: batch_ys})
# calculamos el coste teniendo en cuenta los batches que hay
avg_cost += c / total_batch
# actualizamos el learning_rate igual que lo hace tensorflow
current_lr = current_lr * (1-lr_decay)
# guardamos nuestro coste en el histórico
costs.append(avg_cost)
# Imprimimos las iteraciones
# current_lr = learning_rate * (1-lr_decay) ** (epoch * batch_size + i)
print("[{}] cost: {} lr: {}".format(epoch, avg_cost, current_lr))
print("Entrenamiento finalizado")
# comprobamos lo que ha aprendido nuestra red
correct_prediction = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
# calculamos el accuracy (precisión)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print("Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))
# veamos nuestra función de pérdidas con respecto a las épocas ejecutadas
plt.plot(np.arange(0, n_epochs), costs)
plt.title("Training Loss")
plt.xlabel("Epoch #")
plt.ylabel("Loss")
# probamos la tanh, weights = 1, bias = 1 y loss_fn = mse
activation_function = tf.nn.tanh
learning_rate = 0.1
lr_decay = 1e-3
n_epochs = 10
batch_size = 128
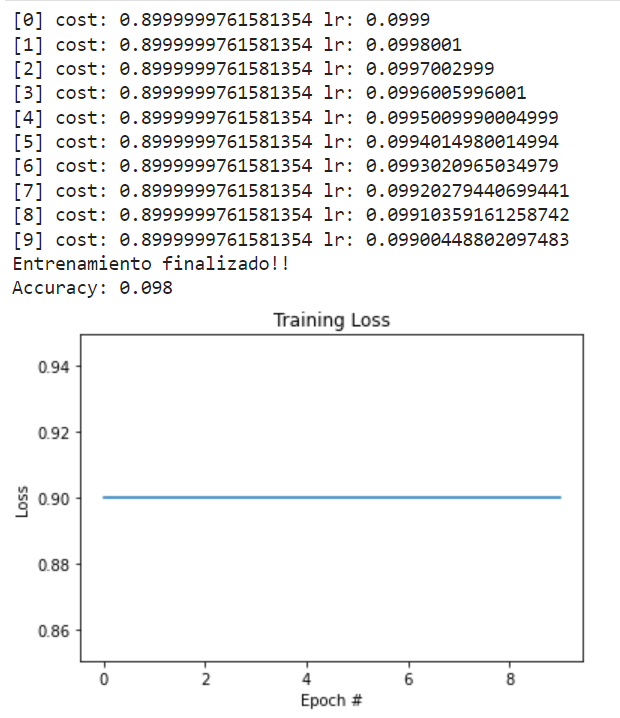
train_network_decay_fnact_w1_b1_mse(activation_function, learning_rate, lr_decay, batch_size, n_epochs)
Conoce más sobre el manejo Big Data
En este post, te hemos expuesto cuáles son los tipos de inicialización de pesos en Deep Learning por medio de ejemplos prácticos, sin embargo, resulta necesario ahondar en este conocimiento.
Es por esto que nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning es ideal para que avances con tu formación. Así, conocerás más sobre los tipos de inicialización de pesos en Deep Learning y las herramientas más importantes para el procesamiento de los macrodatos. Todo ello de forma tanto teórica como práctica y con el acompañamiento de grandes profesionales y expertos en el universo del Big Data. ¿A qué esperas para empezar?











