En este post realizaremos un análisis comparativo entre LDA y GLM por medio de un ejercicio de regresión logística.
Recordemos que la regresión logística o logistic regression es un proceso de modelado que sirve para calcular la probabilidad de resultado discreto dada una variable de entrada. Se usa mucho cuando la variable dependiente o variable objetivo es también una variable categórica.
También cabe recordar dos conceptos importantes, el de LDA y GLM.
Por un lado, el LDA es un fenómeno estadístico en el que se trata de realizar una reducción de similitud. Es diferente al PCA ya que, mientras que este último es aprendizaje no supervisado, el LDA corresponde al aprendizaje supervisado.
Por otro lado, el GLM o Generalized Linear Model (modelo lineal generalizado) es una forma de regresión lineal más flexible en la que están permitidas variables de respuesta que tienen modelos de distribución de errores diferentes a los de una distribución normal.
¿Qué encontrarás en este post?
ToggleAnálisis comparativo entre LDA y GLM
Regresión logística
Vamos a hacer una comparación entre el LDA y GLM por medio del ejercicio de regresión logística. La regresión logística forma parte del conjunto de modelos lineales generalizados o GLM:
#l <- lda (group~ x1 + x2, data = df) model_glm <- glm (group~ x1 + x2, data = df, family = binomial) model_glm betalg <- model_glm$coefficients
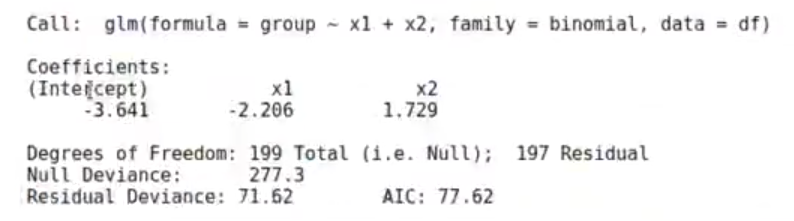
Aquí tenemos una beta, que pertenece a los coeficientes.
Recordemos que significaban estos coeficientes:
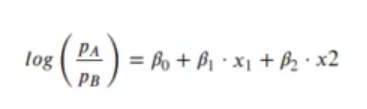
Los coeficientes son los logaritmos de la razón de momios.
El umbral de decisión de una clase u otra lo tenemos en:
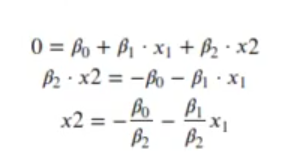
El umbral de decisión entre una LDA y GLM podemos sacarlo igualando a 0, poniendo el umbral en 0, que era el que mejor nos separaba las clases.
Nos daban x2, que sería y dependería de x1. Cuando igualáramos a 0, este nos daría la recta del umbral.
gl <- ggplot (df, aes (x = x1, y = x2, color = group)) + geom_point (size = 0.1) + geom_abline (slope = w [2] / w [1]) + geom_abline (intercept = -betalg [1] / betalg [3], slope = -betalg [2] / betalg [3], color = "blue") gl
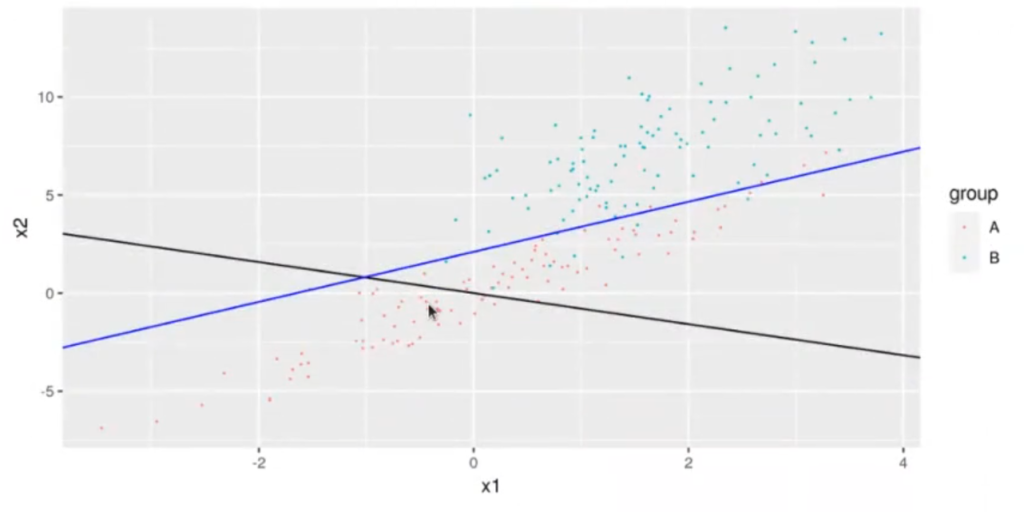
Aunque no lo parezca por la perspectiva de la gráfica, ambas rectas, la de LDA y GLM, son ortogonales, es decir, perpendiculares.
Aquí estamos pintando, por un lado, la curva de proyección (señalada en negro); por el otro, tenemos la recta que nos separa mejor ambas fronteras, ambos grupos de datos (representada por la línea azul).
El vector que define la pendiente de la curva dada por ẞ es el mismo que el vector w:
model_glm$coefficients
(Intercept): -3.64138831593012
x1: -2 20557834669907
x2: 1.72851391746238
Estos son los coeficientes que tenemos.
b <- mode_glm$coefficients [c ("x1", "x2")]
b <- b / sqrt (sum (b ^ 2))
b
x1: -0.787087556350948
x2: 0.616841291287713
Si tratáramos los coeficientes como el vector w, sobre el que estamos proyectando, al final en ambas, en LDA y GLM, son casi los mismos coeficientes que teníamos antes.
No encajan por decimales, pero se parecen mucho.
w
| x1 -0.7841725 |
| x2 0.6205429 |
df_glm <- df
df_glm$pred <- predict (model_glm, df)
g1 <- ggplot (df_glm, aes (x = pred, color = group)) + geom_density () + ggtitle ("GLM")
df$projection <- as matrix (df [ , 2 : 3]) %*% w#l$scaling# w
#dtsprojection <- predict (l, df) $x + th
g2 <- ggplot (df, aes (x = projection, color = group)) + geom_density () + ggtitle ("LDA")
ggarrange (gl, g2, ncol = 2)
La parte importante de todo este asunto son las proyecciones.
A continuación tenemos el resultado de la proyección de LDA y GLM. Los resultados son prácticamente los mismos; lo único que cambia es el umbral, que antes estaba en 0, y en el LDA ahora está en el valor de th.
Dependiendo del valor que le queramos poner va a cambiar un poco. Si ponemos, por ejemplo, solo la predicción, el umbral de la proyección LDA sí que va a quedar en 0.
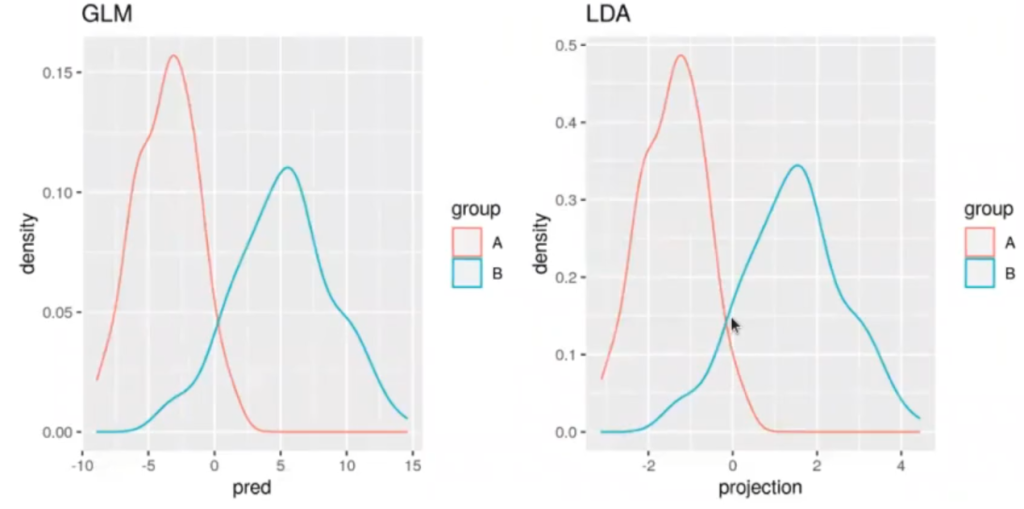
Si nos fijamos detenidamente, podemos notar que el resultado del predict de la LDA y GLM no es exactamente el mismo. Se parece muchísimo, pero no es del todo igual, no termina de encajar.
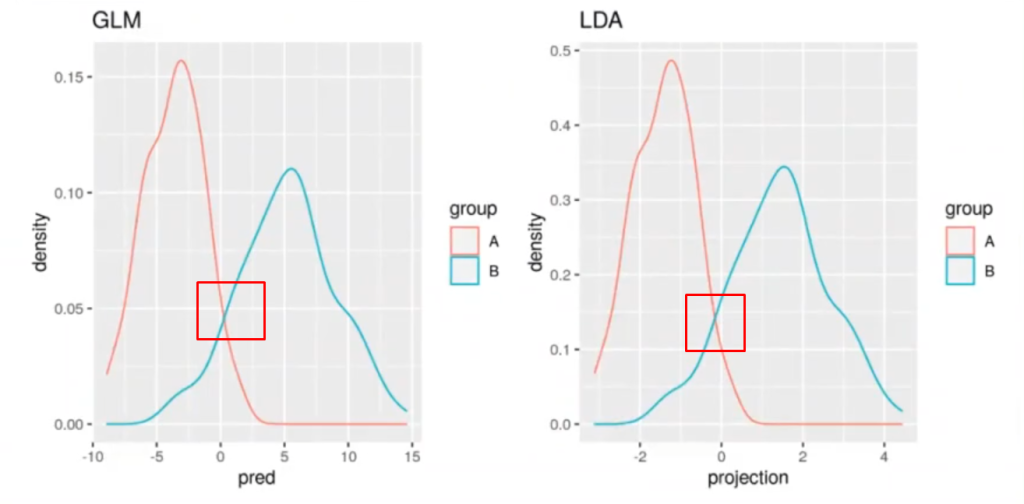
Esto sucede porque uno está intentando minimizar el error cuadrático medio y el otro está tratando de separar los puntos. No obstante, esto no cobra mayor relevancia, ya que ambos son equivalentes y se puede trabajar con ellos.
Ahora que hemos aprendido un poco sobre el LDA y GLM y que hemos hecho una comparación de ambos por medio de un modelo de regresión logística, podemos pasar al siguiente nivel. Para ello, KeepCoding te ofrece el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos necesarios para poder incursionar rápidamente en el mercado laboral. ¡Anímate a impulsar tu vida y solicita más información!











