Coeficiente de determinación R² en estadística

El coeficiente de determinación R² en estadística es uno de los cálculos que siguen al modelo que implementes en tu procesamiento de los macrodatos. En efecto, contar con este tipo de conocimiento te ayudará a comprender el principal propósito de la estadística, es decir, entender las variables y las diferentes relaciones que se encuentran entre ellas.

De hecho, este tipo de cálculos cumplen el propósito de facilitar los procesos y asegurar resultados más precisos, gracias a los que se destaca el valor de la información. Por este motivo, en este post, te explicamos qué es y cómo funciona el coeficiente de determinación R² en estadística para el manejo de los macrodatos.

Coeficiente de determinación R² en estadística

El coeficiente de determinación R² en estadística proporciona una medida que te permite saber lo bien que la medida sigue al modelo utilizado. En suma, este estadístico se calcula por medio de la siguiente fórmula:

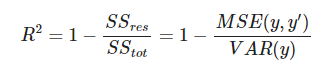
En la que:

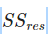
es la suma del cuadrado de los residuos:

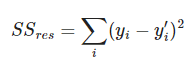
Además:

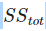
es proporcional a la varianza de Y:

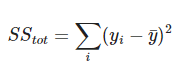
De esta forma, el coeficiente de determinación R² en estadística determina que cuanto más cercano a 1, mejor seguirá la predicción a los datos reales.

Por otra parte, responde a la pregunta: ¿cómo de mejor es mi modelo respecto a uno que siempre devuelva el valor medio?

Rsq <- 1-(sum((Y-est_Y)^2))/(sum((Y-mean(Y))^2))
print(paste("El coeficiente de determinación es:",Rsq))

[1] “El coeficiente de determinación es: 0.985188061001936”

summary(model)

A continuación, para que profundices en cómo funciona el coeficiente de determinación R² en estadística, te exponemos otro ejemplo:

options(repr.plot.height=4,repr.plot.width=6)
n<-40
xn<-rnorm(n,sd=1)
yn<-xn*2+rnorm(n,mean=2,sd=1)
datos<-data.frame(y=yn,X=xn)
model=lm(datos, formula=y~X+0)


plot(xn,yn,col="blue")
abline(c(0,model$coefficients),col="red")
summary(model)$r.squared

0.493914310299537

Esto llevado a la esquematización apunta a un gráfico de dispersión que sería el siguiente:

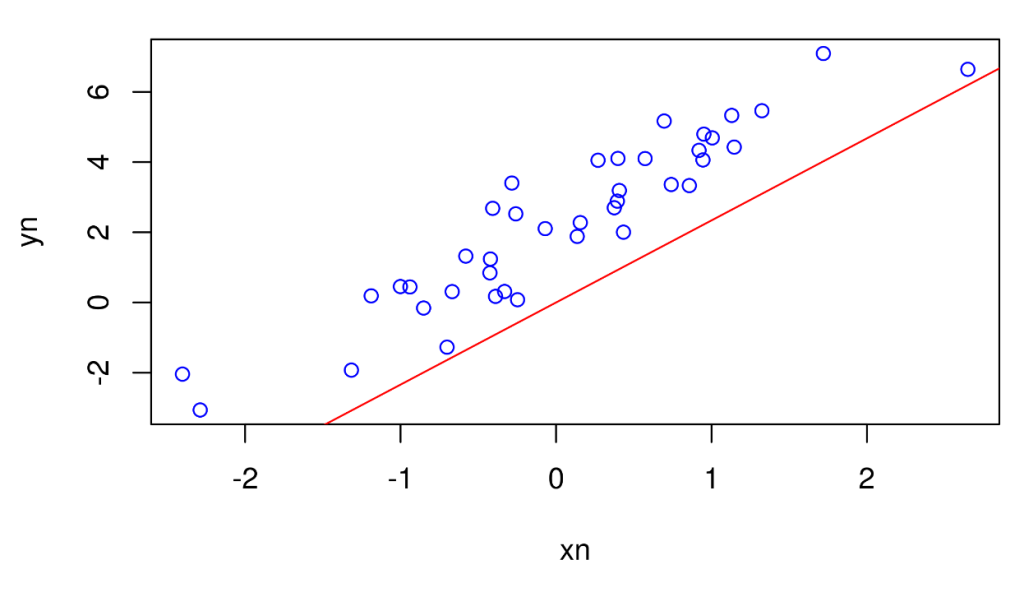
summary(model)

options(repr.plot.height=2,repr.plot.width=6)

vcov_matrix<-as.numeric(t(model$residuals)%*%model$residuals/(length(model$residuals)-2))*solve(t(xn)%*%xn)


ggplot(data=datos, aes(x=X)) +     
    stat_function(fun=mydt,args = list(df = df,mn=model$coefficients[1],sd=sqrt(diag(vcov_matrix))[1]),color="#2222BB")+
    geom_vline(xintercept=qt(0.975,df)*sqrt(diag(vcov_matrix))[1]+model$coefficients[1])+
    geom_vline(xintercept=qt(0.025,df)*sqrt(diag(vcov_matrix))[1]+model$coefficients[1])+
    xlim(-20,20)

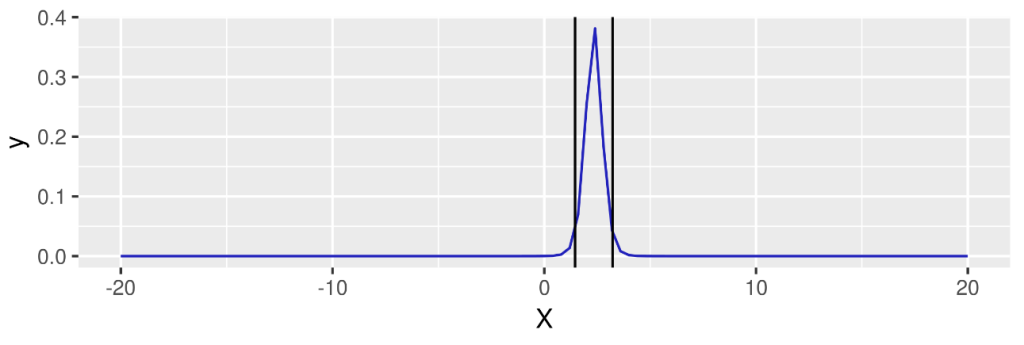
cnf_int<-confint(model)
cnf_int

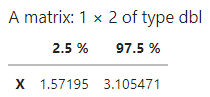
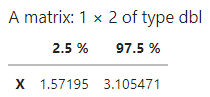
options(repr.plot.height=4,repr.plot.width=6)

datos<-datos[order(datos$X),]
pred<-predict(model,datos,interval="confidence")
est_Y <- pred[,"fit"]
plot(xn,yn,col="blue")
points(datos$X,est_Y,col="red")

#lines(datos$X,pred[,"fit"],col="red")
#lines(datos$X,pred[,"lwr"],col="black")
#lines(datos$X,pred[,"upr"],col="black")
#abline(c(0,cnf_int[2]),col="gray")
#abline(c(0,cnf_int[1]),col="gray")

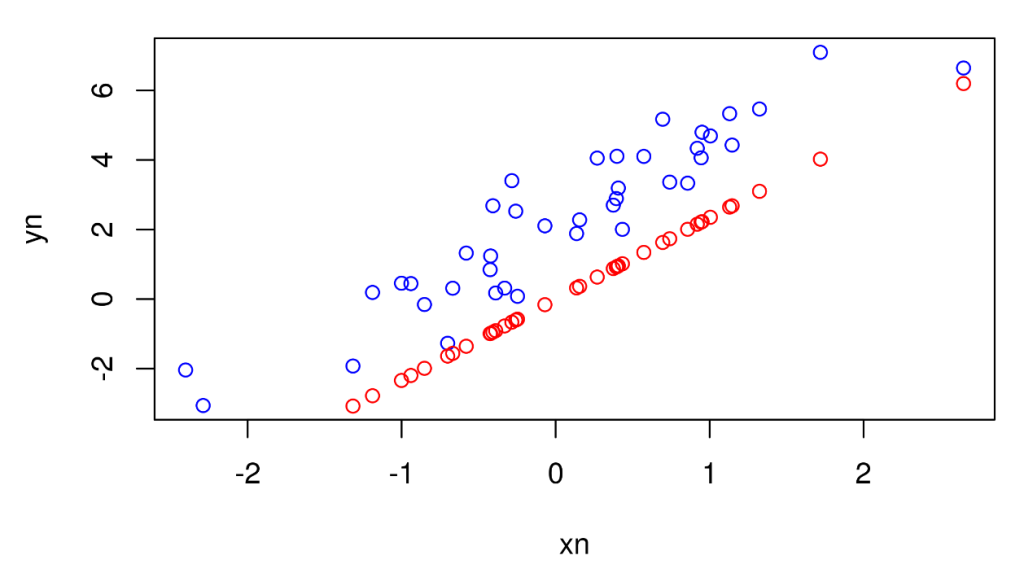
Por último, te animamos a seguir practicando este cálculo de coeficiente de determinación R² en estadística por medio de más ejemplos prácticos.

A través de este post, has podido identificar qué es el coeficiente de determinación R² en estadística para Big Data. No obstante, este desarrollo exige continuar practicando para ganar experiencia. Si no tienes claro cómo puedes empezar, ¡desde KeepCoding te traemos la mejor opción!

Nuestro Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning cuenta con once módulos que te prepararán y pondrán a prueba tus destrezas con las principales herramientas desarrolladas para el procesamiento de los macrodatos en el transcurso de sus 11 módulos. Para ello, también contarás con el apoyo de una serie de expertos en Big Data que te guiarán en los procesos tanto teóricos como prácticos. ¡No esperes más, inscríbete y empieza ahora!