¿Sabías que se puede aplicar cosine similarity en espacios vectoriales? En un ejercicio sobre espacios vectoriales realizado en otro post, modelamos algunos prototipos de coches en un espacio vectorial. Los datos que teníamos eran:
| Modelo | Precio (€) | Velocidad máxima | Tiempo de aceleración |
| Porsche Taycan | 110000 | 280 km/h | 3.8 s |
| Tesla3 | 90000 | 260 km/h | 3.5 s |
| BMW i3 | 60000 | 160 km/h | 7 s |
Con estos datos construimos un espacio vectorial para los tres modelos con las diferentes características que estos representaban:
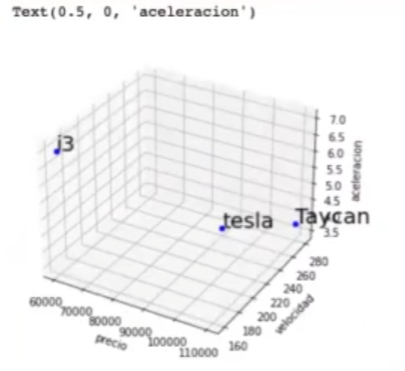
Ahora, veamos un ejercicio de cosine similarity en espacios vectoriales y tratemos de medir la similitud entre los distintos coches que tenemos en nuestro espacio vectorial.
Cosine similarity en espacios vectoriales
Para este ejercicio de cosine similarity en espacios vectoriales vamos a hacer uso de la librería sklearn, que tiene implementado internamente el cosine similarity.
Lo primero que haremos será importar la librería que necesitamos. El StandardScaler es necesario, porque hay que estandarizar. También tendremos que definir el scaler, posteriormente le introduciremos x (esto lo hacemos con el .fit).
Hasta aquí lo único que hemos hecho es calcular la media y la varianza de nuestros datos. Ahora, con transform, se lo estaríamos aplicando a nuestros datos. Lo que hace transform es transformar los datos usando la media y la varianza calculada con anterioridad.
#cosine similarity en espacios vectoriales
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler ()
#scaler.fit (X) #Calcular media y varianza de nuestros datos por columna
#X_scaler = scaler.transform (X)
X_scaler = scaler.fit_transform (X)
print (X_scaler)
Si imprimimos esto, vemos cómo han cambiado bastante los datos.
[[1.13554995 0.88900089 -0.61028968]
[0.16222142 0.50800051 -0.79968993]
[-1.29777137 -1.3970014 1.40997962]]
Los datos de antes eran 110000, 90000, 60000, etc. Ahora vemos que casi todos los datos que nos han resultado están entre la media y apreciamos cómo el rango de valores es muy parecido.
Para calcular la similitud, vamos a usar cosine similarity en espacios vectoriales. Le vamos a introducir al cosine similarity, entre paréntesis, los valores escalados y los valores escalados, es decir, los valores escalados dos veces.
#cosine similarity en espacios vectoriales
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler ()
#scaler.fit (X) #Calcular media y varianza de nuestros datos por columna
#X_scaler = scaler.transform (X)
X_scaler = scaler.fit_transform (X)
print (X_scaler)
print ('\n')
#Calcular similitud
similarities = cosine_similarity (X_scaler, X_scaler)
print (similarities)[[1. 0.74666083 -0.96296773]
[0.74666083 1. -0.89836063]
[-0.96296773, -0.89836063 1. ]]
Le hemos pasado dos parámetros que son la misma cosa. El primero lo que hará será imprimirnos una matriz.
Vamos a visualizarlo en una tabla:
| Modelos | Taycan | Tesla | i3 |
| Taycan | 1 | 0.746 | -0.624 |
| Tesla | 0.746 | 1 | -0.898 |
| i3 | -0.962 | 0.898 | 1 |
Podemos ver que los modelos Taycan y Tesla son más parecidos entre ellos y que poco tienen de similitud el Taycan o el Tesla con el i3. Dada la anterior tabla, podemos observar que Taycan y Taycan, Tesla y Tesla e i3 e i3 son iguales, por eso la similitud es igual a 1.
Con esta función la similitud da entre -1 y 1, no entre 0 y 1, como se podría llegar a pensar.
Observamos que la similitud entre el Tesla y el Taycan es de 0.746, pero la similitud entre el Taycan y el i3 es -0.962; esto significa que es muy dispar. Asimismo, tenemos que la relación entre el Tesla y el i3 es -0.898, que también es muy dispar.
Ahora que hemos visto cómo funciona la estructura de un espacio vectorial, puedes seguir aprendiendo sobre Big Data, una de las disciplinas más demandadas hoy en día. Para ello, entra a nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, la formación intensiva e íntegra en la que podrás adquirir todos los conocimientos teóricos y prácticos necesarios para adentrarte en el mercado laboral en poco tiempo. ¡Anímate a impulsar tu carrera laboral y solicita ya mismo más información!











