En otro artículo hemos probado la relación que existe entre la transformación lineal y las matrices. En esta ocasión, veremos un ejemplo de matrices en la transformación lineal para entender un poco mejor estos dos conceptos básicos en matemáticas y, por tanto, en el mundo del machine learning.
Matrices en la transformación lineal: un ejemplo
Supongamos que tenemos la siguiente matriz:
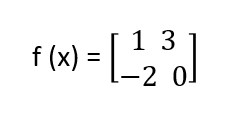
Hemos dicho que esta matriz nos ayuda en la transformación. Es decir, lo que nos está indicando la matriz asociada es dónde acaba la transformación lineal, cuál es el final de los componentes del eje x y del eje y.
También habíamos mencionado que la transformación lineal recibía un input y nos entregaba un output. De modo que:
[ | ] → f (x) → [ | ]
Vamos a hacer una prueba para corroborar que esta información es cierta. El vector más simple que podemos usar es x, y (1, 1):
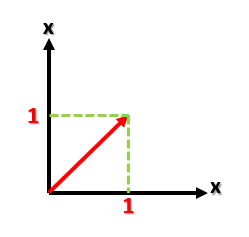
Este vector, que está definido por (1, 1), se lo vamos a introducir a nuestra transformación lineal, que viene dada por la matriz [1 3 -2 0]. Nos va a devolver un nuevo vector, que no sabemos cuál es, pero que calcularemos enseguida.
¿Qué haremos ahora? La matriz, cuya primera columna corresponde al eje x y segunda columna al eje y, la podemos escribir del siguiente modo:
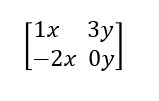
Si a esto le sustituimos los valores, tenemos que el numerador del vector es el eje x y el denominador del vector es el eje y. De modo que la matriz quedaría como:

La matriz resultante del desarrollo de estas operaciones sería:
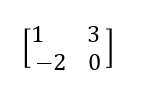
Este resultado hay que sumarlo. Es decir, desarrollamos la suma de 1+3 y de -2+0. El resultado sería: [4/-2].
Entonces, a esta transformación le hemos introducido [1/1] y nos ha dado como resultado [4/-2]. Veamos cuál sería el gráfico correspondiente:
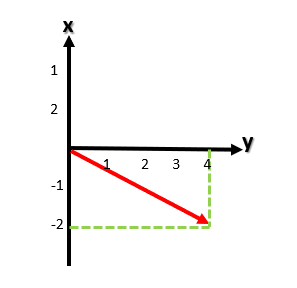
De modo que la transformación lineal que tendríamos sería:
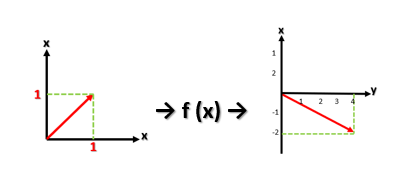
Esta transformación venía dada por la matriz:
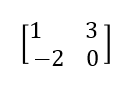
Las ecuaciones
Acerquémonos a las ecuaciones resultantes en la matriz. Tenemos dos ecuaciones:
- 1x + 3y
- -2x + 0y
El 1 de la primera ecuación sale del primer valor de la matriz que tenemos, es decir, el número que se encuentra en la primera fila y la primera columna de la misma.
El 3 de la primera ecuación sale del valor perteneciente a la primera fila y segunda columna de la matriz en cuestión.
El -2 de la segunda ecuación es el que se encuentra en la primera fila y la primera columna de la matriz.
Y por último, el 0 de la segunda ecuación es el que se encuentra en la primera fila y en la segunda columna de la matriz.
Cuando sustituimos los valores de x e y en ambas ecuaciones, nos quedan otros valores, que son:
- 1 . 1 + 3 . 1
- -2 . 1 + 0
El punto representa el símbolo de multiplicación. Asimismo, los 1 por los que son reemplazados los valores de x e y provienen del vector (1, 1) que propusimos en el inicio de este ejercicio de matrices en la transformación lineal.
Los resultados de multiplicar
- 1 x 1 + 3 x 1
y
- -2 x 1 + 0
son:
- 1 + 3 = 4
- -2 + 0 = -2
De ahí que el valor de la matriz final sea [4/-2].
Representación de las matrices en la transformación lineal
Existen dos formas de representar las matrices en la transformación lineal:
- Supongamos que tenemos el vector [1/1]. Si queremos multiplicar el valor del vector por la matriz anterior, podríamos hacerlo así:
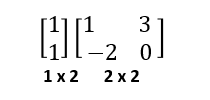
- La otra forma sería agarrar la matriz y hacer la operación que hemos hecho con el ejercicio anterior.
Con ambas formas obtendremos los mismos resultados. De hecho, si hacemos la sustitución como en el primer ejemplo, obtendremos las mismas ecuaciones que en la segunda forma.
Si quieres acceder a una de las disciplinas más demandadas y mejor pagadas en todo el mercado laboral, no te pierdas el Big Data Bootcamp, una formación íntegra y de alta intensidad en la que adquirirás, en pocos meses, todos los conocimientos teóricos y prácticos que te ayudarán a obtener el trabajo de tus sueños. ¡Entra ya para solicitar información y anímate a cambiar tu futuro de la mano de los mejores profesionales!











