Un ejemplo de una red neuronal profunda en TensorFlow te ayudará a comprender con más profundidad y desde la práctica cómo se implementan las redes neuronales profundas dentro del manejo de los macrodatos.
Por ello, en este post, te presentamos un ejemplo de una red neuronal profunda en TensorFlow.
Ejemplo de una red neuronal profunda en TensorFlow
A partir de dos capas ocultas en adelante es cuando podemos hablar de redes neuronales profundas, como en red neuronal TensorFlow. Ahora vamos a realizar una nueva modificación en nuestra función (debemos definirla en una nueva celda con las modificaciones).
Concretamente, para este ejemplo de una red neuronal profunda en TensorFlow vamos a darle más profundidad a nuestra red añadiendo tres capas ocultas más, además de las que ya tenemos; es decir, en el ejemplo TensorFlow, nuestra deep net estará compuesta por la entrada, cuatro capas ocultas con 200, 100, 60 y 30 neuronas, respectivamente, y la capa de salida con las 10 neuronas.
Además, vamos a hacer dos modificaciones más y vamos a extraer como parámetros de entrada a la función la capa de activación de las hidden layers y el optimizador. Con estos cambios, el nuevo método tendrá la siguiente cabecera en la red neuronal TensorFlow:
def train_deep_net(learning_rate, batch_size, num_epochs, act_function, optimizer)Para el ejemplo TensorFlow, donde expondremos el de una red neuronal profunda en TensorFlow, copia y pega el código de la función anterior en una nueva celda, añade tres capas ocultas extra y modifica la función de activación y el optimizador según el parámetro de entrada a la función.
def train_deep_net(learning_rate, batch_size, num_epochs, act_function, optimizer):
# Creamos placeholders para almacenanar los datos de entrada y los labels
X = tf.placeholder(tf.float32, [None, 784]) #(X) # Imágenes del mnist: 28*28 = 784
Y_true = tf.placeholder(tf.float32, [None, 10]) #(X) # Número indicando la clase 0-9 => 10 clases
# Creamos e inicializamos las variables W y b con valores aleatorios que sigan una distribución normal de las redes neuronales profundas.
W1 = tf.Variable(tf.truncated_normal([784, 200], stddev=0.1)) #(X)
B1 = tf.Variable(tf.zeros([200])) #(X)
W2 = tf.Variable(tf.truncated_normal([200, 100], stddev=0.1)) #(X)
B2 = tf.Variable(tf.zeros([100])) #(X)
W3 = tf.Variable(tf.truncated_normal([100, 60], stddev=0.1)) #(X)
B3 = tf.Variable(tf.zeros([60])) #(X)
W4 = tf.Variable(tf.truncated_normal([60, 30], stddev=0.1)) #(X)
B4 = tf.Variable(tf.zeros([30])) #(X)
W5 = tf.Variable(tf.truncated_normal([30, 10], stddev=0.1)) #(X)
B5 = tf.Variable(tf.zeros([10])) #(X)
# Calculamos las predicciones en el ejemplo TensorFlow o redes neuronales profundas:
Y1 = act_function(tf.matmul(X,W1) + B1) #(X)
Y2 = act_function(tf.matmul(Y1,W2) + B2) #(X)
Y3 = act_function(tf.matmul(Y2,W3) + B3) #(X)
Y4 = act_function(tf.matmul(Y3,W4) + B4) #(X)
Y_logits = tf.matmul(Y4,W5) + B5
Y_pred = tf.nn.softmax(Y_logits)
# Ahora, en el ejemplo de una red neuronal profunda en TensorFlow definimos función de pérdidas (Cross_entropy)
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=Y_logits, labels=Y_true))
#loss = tf.reduce_mean(-tf.reduce_sum(Y_true * tf.log(Y_pred), reduction_indices=1)) #(X)
#loss = tf.reduce_mean(-tf.reduce_sum(Y_true*tf.log(Y_pred), reduction_indices=1))
# Optimizador SGD de las redes neuronales TensorFlow.
train = optimizer(lr).minimize(loss) #(X)
# % de predicciones correctas en un determinado batch (i.e. accuracy) de las redes neuronales profundas.
is_correct = tf.equal(tf.argmax(Y_pred,1), tf.argmax(Y_true,1))
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
def train_deep_net(learning_rate, batch_size, num_epochs, act_function, optimizer):
# Creamos placeholders para ir almacenando los datos de entrada y los labels
X = tf.placeholder(tf.float32, [None, 784]) #(X) # Imágenes del mnist: 28*28 = 784
Y_true = tf.placeholder(tf.float32, [None, 10]) #(X) # Número indicando la clase 0-9 => 10 clases
# Creamos e inicializamos las variables W y b con valores aleatorios que sigan una distribución normal para las redes neuronales TensorFlow.
W1 = tf.Variable(tf.truncated_normal([784, 200], stddev=0.1)) #(X)
B1 = tf.Variable(tf.zeros([200])) #(X)
W2 = tf.Variable(tf.truncated_normal([200, 100], stddev=0.1)) #(X)
B2 = tf.Variable(tf.zeros([100])) #(X)
W3 = tf.Variable(tf.truncated_normal([100, 60], stddev=0.1)) #(X)
B3 = tf.Variable(tf.zeros([60])) #(X)
W4 = tf.Variable(tf.truncated_normal([60, 30], stddev=0.1)) #(X)
B4 = tf.Variable(tf.zeros([30])) #(X)
W5 = tf.Variable(tf.truncated_normal([30, 10], stddev=0.1)) #(X)
B5 = tf.Variable(tf.zeros([10])) #(X)
# Calculamos las predicciones del ejemplo de una red neuronal profunda en TensorFlow
Y1 = act_function(tf.matmul(X,W1) + B1) #(X)
Y2 = act_function(tf.matmul(Y1,W2) + B2) #(X)
Y3 = act_function(tf.matmul(Y2,W3) + B3) #(X)
Y4 = act_function(tf.matmul(Y3,W4) + B4) #(X)
Y_logits = tf.matmul(Y4,W5) + B5
Y_pred = tf.nn.softmax(Y_logits)
# Definimos función de pérdidas (Cross_entropy) de la red neuronal TensorFlow
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=Y_logits, labels=Y_true))
#loss = tf.reduce_mean(-tf.reduce_sum(Y_true * tf.log(Y_pred), reduction_indices=1)) #(X)
#loss = tf.reduce_mean(-tf.reduce_sum(Y_true*tf.log(Y_pred), reduction_indices=1))
# Optimizador SGD de las redes neuronales TensorFlow.
train = optimizer(lr).minimize(loss) #(X)
# % de predicciones correctas en un determinado batch (i.e. accuracy)
is_correct = tf.equal(tf.argmax(Y_pred,1), tf.argmax(Y_true,1))
accuracy = tf.reduce_mean(tf.cast(is_correct, tf.float32))
# Gráficar losses por época
plt.plot(np.arange(0, n_epochs), loss_epoch_tr) #(X)
plt.plot(np.arange(0, n_epochs), loss_epoch_val)
plt.legend(['train', 'val'], loc='upper left')
plt.title('Training Loss') #(X)
plt.xlabel('Epoch #') #(X)
plt.ylabel('Loss') #(X)
b_size = 128
n_epochs = 50
lr = 0.005
act_function = tf.nn.relu
#optimizer = tf.train.GradientDescentOptimizer
optimizer = tf.train.AdamOptimizer
train_deep_net(lr, b_size, n_epochs, act_function, optimizer)
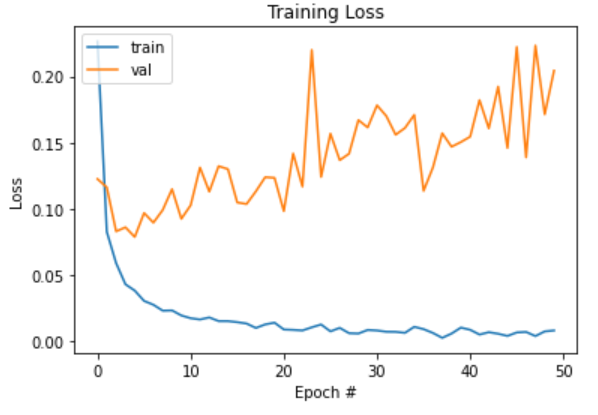
Así, habrás conocido las redes neuronales profundas en TensorFlow.
En este post, te hemos expuesto un ejemplo de una red neuronal profunda en TensorFlow. Sin embargo, debes tener en cuenta que este proceso requiere de una gran constancia en el ensayo. Por ello, te animamos a seguir practicando. Si aún no sabes cómo, en KeepCoding te ofrecemos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning.
Por medio de esta formación de alta calidad, se te presentarán las teorías del aprendizaje automático con énfasis en algoritmos de regresión y clasificación. De manera que, con el tiempo, serás capaz de conocer las ventajas y desventajas de los distintos algoritmos analizados. Además, adquirirás experiencia gracias a que se fusionan los fundamentos con ejemplos prácticos y realistas para que puedas aplicarlos. ¡Pide información, inscríbete ahora y sigue aprendiendo!











