En este artículo veremos algunos ejemplos de árboles de decisión sintéticos en clasificación. Existen tres tipos de árboles:
- Árboles de clasificación sobre ejemplos sintéticos.
- Árboles de clasificación sobre ejemplo realista.
- Árboles de regresión.
En esta ocasión, nos centraremos en el primer tipo.
Ejemplos de árboles de decisión sintéticos en clasificación
Lo primero que haremos será cargar las librerías necesarias:
#Ejemplos de árboles de decisión
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
% matplotlib inline
cm = plt.cm.RdBu
cm_bright = ListedColormap (['#FF0000', '#0000FF'])
import warnings
warnings.filterwarnings ('ignore')Luego algunos ajustes:
#Ejemplos de árboles de decisión
#definimos una función para representar el resultado del ajuste def plot_decision_boundary (x, y, h, model):
x_min, x_max = X [ : , 0].min () - .5, X [ : , 0].max () + .5
y_min, y_max = X [ : , 1].min () - .5, X [ : , 1].max () + .5
h = .05 #step size in the mesh
xx, yy = np.meshgrid (np.arange (x_min, x_max, h), np.arange (y_min, y max, h))
model = model.fit (x, y)
Zd= model.predict (np.c_[xx.ravel (), yy, ravel ()])
Zd = Zd.reshape (xx.shape)
Zp = model.predict_proba (np.c_[xx, ravel (), yy.ravel ()]) [ : , 1]
Zp = Zp.reshape (xx.shape)#ejemplos de árboles de decisión.
#Ejemplo 1
ejemplo1 = pd.read csv ("./data/ex2data1.txt", sep = " , ", header = None, names = ['x1', 'x2', 'label'])
#Ejemplo 2
ejemplo2 = pd.read csv ("./data/ex2data2.txt",sep = " , ", header = None, names = ['x1', 'x2', 'label'])
#Ejemplo 3: Problema XOR
np.random.seed (0)
# -- parameters
N = 800
mu = 1.5 #Cambia este valor
sigma = 1 #Cambia este valor
#variables auxiliares
unos = np.ones (int (N / 4))
random4 = sigma * np.random.randn (int (N / 4), 1)
random2 = sigma * np.random.randn (int (N / 2), 1)
# -- features
y3 = np.concatenate ([-1 * unos, unos, unos, -1 * unos])
X1 = np.concatenate ([-mu + random4, mu + random4, -mu random4, mu + random4])
X2 = np.concatenate ([+mu + random2, mu + random2])
X3 = np.hstack ((X1, X2))#Ejemplos de árboles de decisión
plt.figure (figsize = (15, 5))
plt.subplot (1, 3, 1)
plt.scatter (ejemplo1 ['x1'], ejemplo1 ['x2'], c = ejemplo1 ['label'], cmap = cm_bright)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x 25", fontsize = 16)
plt.title ('Ejemplo 1')
plt.subplot (1, 3, 2)
plt.scatter (ejemplo2 ['x1'], ejemplo2 ['x2'], c = ejemplo2 ['label'], cmap = cm_bright)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x 25", fontsize = 16)
plt.title ('Ejemplo 2')
plt.subplot (1, 3, 3)
plt.scatter (X3 [ : , 0], X3 [ : , 1], c = y3, cmap = cm_bright)
plt.xlabel ("$x_1$", fontsize = 16)
plt.ylabel ("$x 25", fontsize = 16)
plt.title ('Ejemplo 3')
plt.tight_layout ()
plt.show ()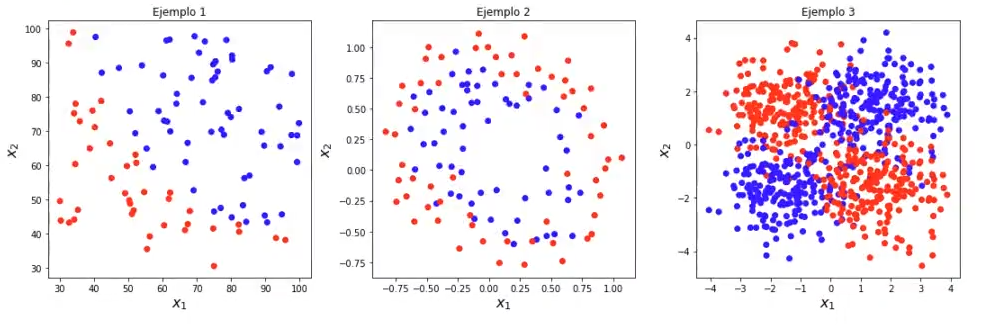
Árboles de decisión de ejemplos
Ejemplo1
Ahora vamos a entrenar un árbol de decisión sobre el ejemplo anterior:
#Ejemplos de árboles de decisión
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
#preparamos los datos
data1 = ejemplo1.values
X1 = data1 [ : , 0 : 2]
y1 = data1[ : , - 1]
#creamos el modelo y ajustamos
treeModell = DecisionTreeClassifier ().fit (x1, y1)
plot_decision_boundary (x1, y1, 0.05, treeModel1)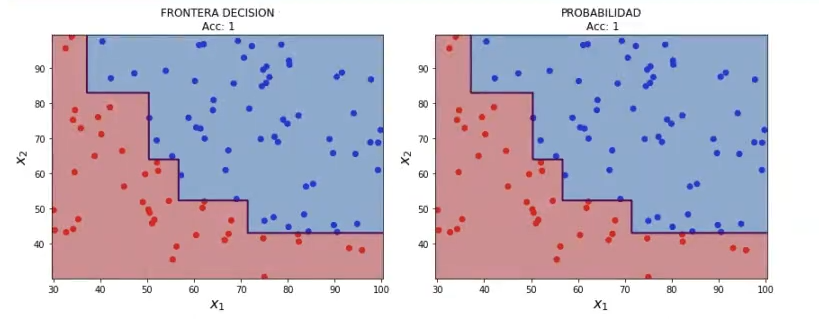
Ejemplo 2
#Ejemplos de árboles de decisión
#Ejemplo 2
#preparamos los datos
data2 = ejemplo2.values
X2 = data2 [ : , 0 : 2]
y2 = data2 [ : , - 1]
#creamos el modelo y ajustamos
treeModel2 = DecisionTreeClassifier ().fit (x2, y2)
plot_decision_boundary (X2, y2, 0.05, treeModel2)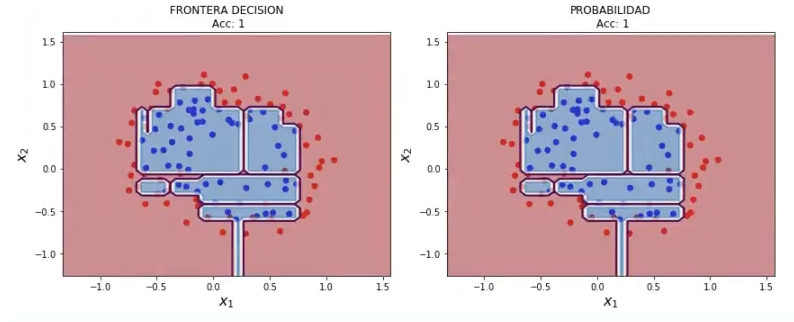
Ejemplo 3
#Ejemplos de árboles de decisión
#Ejemplo 3
#creamos el modelo y ajustamos
treeModel3 = DecisionTreeClassifier ().fit (X3, y3)
plot_decision_boundary (X3, y3, 0.05, treeModel3)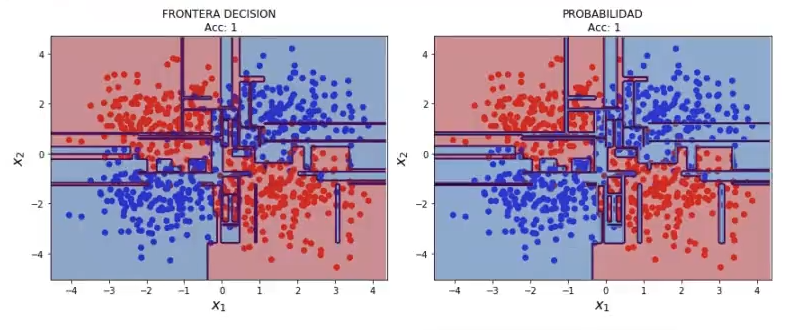
A la vista de los ejemplos anteriores, podemos comprobar varias cosas:
- Seguramente estamos cometiendo overfitting, porque las fronteras de separación son altamente complejas. ¿Cómo podemos controlar la complejidad de un árbol?
- Las prestaciones las estamos midiendo sobre el conjunto de entrenamiento, por lo que no sabemos el alcance real que tienen estos algoritmos.
Los árboles de decisión tienen varios parámetros para controlar la complejidad del mismo. Normalmente, los parámetros más relevantes para controlar la complejidad son:
- Profundidad del árbol (max_depth). Si utilizamos un árbol de profundidad 1, solo podremos dividir el espacio en dos (1 decisión). Si utilizamos un árbol de profundidad 2, tomaremos 4 decisiones, y así sucesivamente. Por tanto, con la profundidad controlamos la complejidad del árbol de decisión. Este parámetro sirve como herramienta regularizar el algoritmo:
- Un árbol de poca profundidad (poco complejo), tendrá menor riesgo de sufrir overfitting a costa de, potencialmente, incurrir en más error de clasificación.
- Un árbol de mucha profundidad (muy complejo), tendrá mayor riesgo de sufrir overfitting a costa de, potencialmente, mejorar el error de clasificación.
- Número mínimo de muestras en una hoja (min_samples_leaf). Podemos forzar a que una hoja tenga un número mínimo de muestras en cada hoja, de forma que:
- Un árbol con un min_samples_leaf elevado tendrá complejidad menor que un árbol con min_samples_leaf pequeño.
¿Qué sigue?
Si quieres seguir aprendiendo sobre Big Data, una de las disciplinas mejor pagadas y más demandadas de la actualidad, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos teóricos y prácticos para incursionar en el mundo tech. ¡Anímate a impulsar tu futuro y solicita más información!











