En este artículo realizaremos un ejercicio con métodos wrapper. Los métodos wrapper son los métodos que utilizan un algoritmo de machine learning como caja negra para rankear distintos subconjuntos de variables de acuerdo a su capacidad predictiva. Normalmente se usan mediante procedimientos hacia delante/atrás en combinación con validación cruzada.
Ejercicio con métodos wrapper
Este ejercicio con métodos wrapper se inspira en 7.10.2 The wrong and right way to do cross-validation, del libro The elements of statistical learning.
Lo que haremos será realizar una clasificación usando el algoritmo de k-nn o vecinos más cercanos. También haremos cross validation, pero en vez de hacerlo con gridsearch, lo haremos con k-folds. La idea de hacer este ejercicio con métodos wrapper con el k-fold, en vez de hacerlo con gridsearch, es realizar el ejercicio de manera incorrecta, para posteriormente poder ver cuál es el camino para hacerlo correctamente.
Como método de filtrado usamos f_classif, solo que, en este caso, como lo estamos haciendo con un modelo, lo que haremos será un rankeo usando este método de filtrado y luego haremos un modelo para evaluar los subconjuntos que ese rankeo dice que son mejores.
Entonces, el f_test de f_classif nos va a dar un subconjunto de características y nosotros, con ese subconjunto, vamos a entrenar un modelo y vamos a tener una mética.
Eso lo haremos 500 veces; vamos a ver qué nos dice.
#Ejercicio con métodos wrapper
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model selection import KFold
from sklearn.feature_selection import f_classif
#This is the WRONG way
np.random.seed (0)
score = [ ]
for i in range (500): #This is run for a number of experiments. Montecarlo simulation
#Create toy example
N = 50
y = np.concatenate ([-1 * np.ones (int (N / 2)), np.ones (int (N / 2))]) #target
X = np.random.randn (N, 5000) #predictors are random variables!
#Note here, the ranking and selection is performed outside the CV loop
f_test, _ = f_classif (x, y)
f_test /= hp.max (f_test)
ranking = np.argsort (f_test) [ : : - 1]
selected = ranking [0 : 50)
Xs = X [ : , selected]
#1 - neighbor classifier
knn = KeighborsClassifier (n_neighbors = 1)
#Ejercicio con métodos wrapper
#5-fold CV
kf = KFoldin_splits = 5, shuffle = True)
score_i = [ ]
for train, validation in kf.split (Xs):
knn.fit (Xs [train, : ], y [train])
accuracy = knn.score (xs [validation, :), y [validation])
score_i.append (accuracy)
score.append (np.mean (score_i))
print ("Error rate (%): " + str (1 - np.mean (score)) * 100))
plt.hist (score)
plt.show ()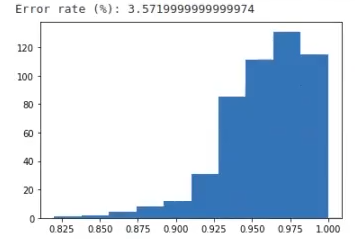
El error medio es 3.57%. Parece demasiado bajo, lo cual indica que hay algo mal, porque incluso tenemos ruido. Es decir, tenemos un error demasiado bajo en un problema que es insoluble. Para que este ejercicio funcione bien, tenemos que hacer el test y quedarnos con los 50 mejores dentro del cross validation.
Veamos cómo podríamos hacerlo bien:
#Ejercicio con métodos wrapper
#This is the right way
np.random.seed (0)
scare = [ ]
for i in range (500): #This run for a number of experiments. Montecarlo simulation
#Create toy example
N = 50
y = np.concatenate ([ -1 * np.ones (int (N/2)), np.ones (int (N/2))]) #target
X = np.random.randn (N, 5000) #predictors, again random variables
#1 - neighbor classifier
knn = KNeighborsClassifier (n_neighbors = 1)
#5 - fold CV
kf = KFold (n_splits = 5, shuffle = True)
score_i = [ ]
for train, validation in kf.split(X):
#Note here, the ranking and selection is performed inside the CV loop
f_test, _ = f_classif (X [train, :], y [train])
f_test /= np.max (f_test)
ranking = np.argsort (f_test) [ : : - 1 ]
selected = ranking [0 : 50]
Xs = X [ : , selected)
#Ejercicio con métodos wrapper
knn.fit (Xs [train, :], y [train])
accuracy = knn.score (Xs [validation, : ].y [validation])
score_i.append (accuracy)
score.append (np.mean (score_i))
print ("Error rate (%): " str ((1 - np.mean (score)) * 100))
plt.hist (score)
plt.show ()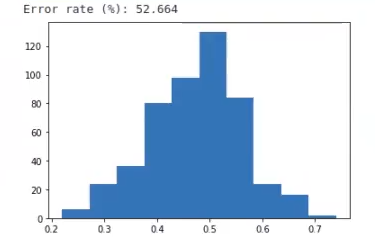
Aquí vemos cómo, cuando lo hacemos bien y metemos el test dentro del cross validation, los resultados cambian mucho.
Observamos que la media de error aumenta exponencialmente, al llegar a un 52.664%, que es, prácticamente, aleatorio.
Este es el resultado que podríamos esperar de un experimento que prácticamente está basado en el azar, donde los datos X no tienen nada que ver con la variable Y.
Uno de los contras de los métodos wrapper es que no tiene equivalencia en scikit learn, es decir, todo lo tendrás que hacer tú mismo y, así como tienes mucho más control, también puedes equivocarte mucho, así que debes tener mucho cuidado.
Ahora que hemos visto un ejercicio con métodos wrapper, podemos dar el siguiente paso en el proceso de aprendizaje sobre una de las disciplinas más prolíficas del momento.
Para esto tenemos el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás todos los conocimientos necesarios para incursionar en el mundo IT. ¡Anímate a cambiar tu vida y solicita ya mismo más información!
