En este post te mostraremos un ejercicio con regresión de Poisson, ¿preparado?
El modelo de regresión de Poisson se usa típicamente para modelar conteo de conjuntos de datos, pero a veces es más relevante modelar el ratio en lugar del conteo.
Así, en lugar de tener la siguiente fórmula, donde y es el conteo esperado para la variable x:
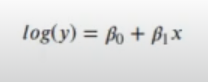
Tenemos esta, donde n es el número de intentos para esa variable x:
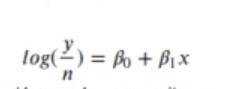
De este modo, la ecuación puede escribirse como:
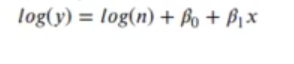
Ese valor de log (n) es lo que se conoce como offset ().
Ejercicio con regresión de Poisson
En otro artículo hemos visto cómo se desarrolla un Test A/B con GLM y cómo se resuelve, dentro de este test, un ejercicio de regresión logística. En este caso haremos lo mismo, pero con una pequeña variación; resolveremos el ejercicio con regresión de Poisson, ya que lo que tenemos son conteos, números de cosas que ocurren.
La regresión de Poisson en la mayoría de ocasiones se utiliza para hacer conteos de datos, pero no nos interesa saber el número de éxitos que hemos tenido. Lo que nos interesa es el ratio de éxito que hemos tenido.
Para eso, lo que nos interesaría ver es el logaritmo de:
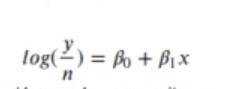
Este equivale al número de intentos, porque cuantos más intentos, mayor va a ser el valor de y. Así, con el doble de visitas en la web podríamos tener el doble de éxitos.
En caso de que utilizáramos esta fórmula:
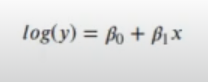
Nos sería completamente inútil la información recogida, ya que esta función lo que nos arrojaría sería el número de clics y lo que necesitamos saber es, de ese número de clics, cuántos fueron casos de éxito.
Así pues, en la fórmula que utilizaremos dividiremos el número de intentos entre el número de aciertos y ese será el log.
El logaritmo del número de intentos se traduce en R como offset.
model <- glm (formula = exitos ~ type + offset (log (intentos)), data = df, family = poisson)
library (jtools)
#plot_summs (model, scale = TRUE, exp= TRUE)
exp(model$coef [2])
exp (confint (model))Este código está intentando predecir el número de éxitos en función del tipo, pero desplazándolo por el número de intentos.
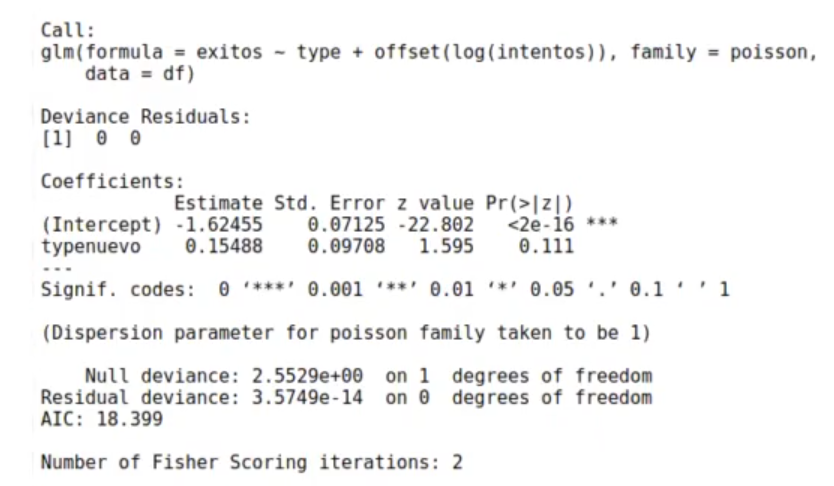
typenuevo: 1.16751269035533
En este ejercicio con regresión de Poisson tenemos el mismo resultado que con el ejercicio anterior. La razón de momios es exactamente igual y la repuesta a la pregunta de cuánto mejora el ratio al cambiar de una web a otra sigue siendo la misma.
exp (confint (model))| 2.5 % | 97.5 % | |
| (Intercept) | 0.1707552 | 0.2258035 |
| typenuevo | 0.9655387 | 1.4130566 |
¿Cuál de los modelos es mejor, teniendo en cuenta el ejercicio con regresión de Poisson y el de regresión logística? No podríamos decirlo con certeza; no obstante, pensamos que es mejor el de Poisson por ser más conservador. Puedes probar ambos a ver cuál se adapta mejor a tus necesidades.
Con el ejercicio con regresión de Poisson resulto, es hora de que tomes la decisión de verificar cuál de los modelos se adapta mejor a ti. Para ello te invitamos a seguir instruyéndote y aprendiendo por medio de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, donde adquirirás todas las bases necesarias para, en muy poco tiempo, incursionar en el mercado laboral. ¡Anímate y solicita más información!











