En este artículo realizaremos un ejercicio de regularización en R para predecir la dureza del hormigón. Para ponernos en contexto, debes saber que el hormigón es el material más importante en la ingeniería civil.
La resistencia a la compresión del hormigón es una función altamente no lineal de la edad e ingredientes. Estos ingredientes incluyen cemento, escoria de alto horno, cenizas volantes, agua, superplastificante, agregado grueso y agregado fino.
Desarrollo de ejercicio de regularización en R
Vamos a empezar con el ejercicio de regularización en R:
In [ ] : concrete <- read.csv ("data/Concrete_Data.csv",
col.names = c ("cemento", "escoria", "cenizas", "agua", "plastificante", "aggrueso", "agfino", "edad", "resistencia")
head (concrete)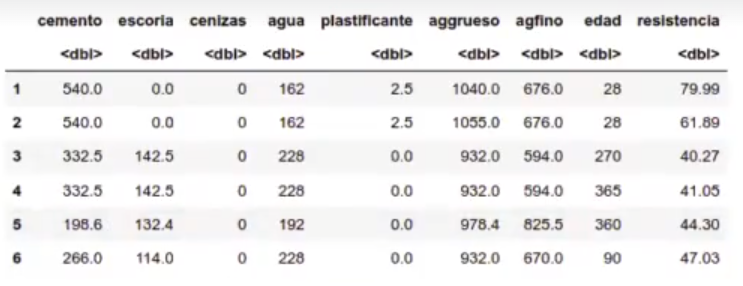
In [ ] : options (repr.plot.height = 5, repr.plot.width = 8, repr.plot.res = 200)
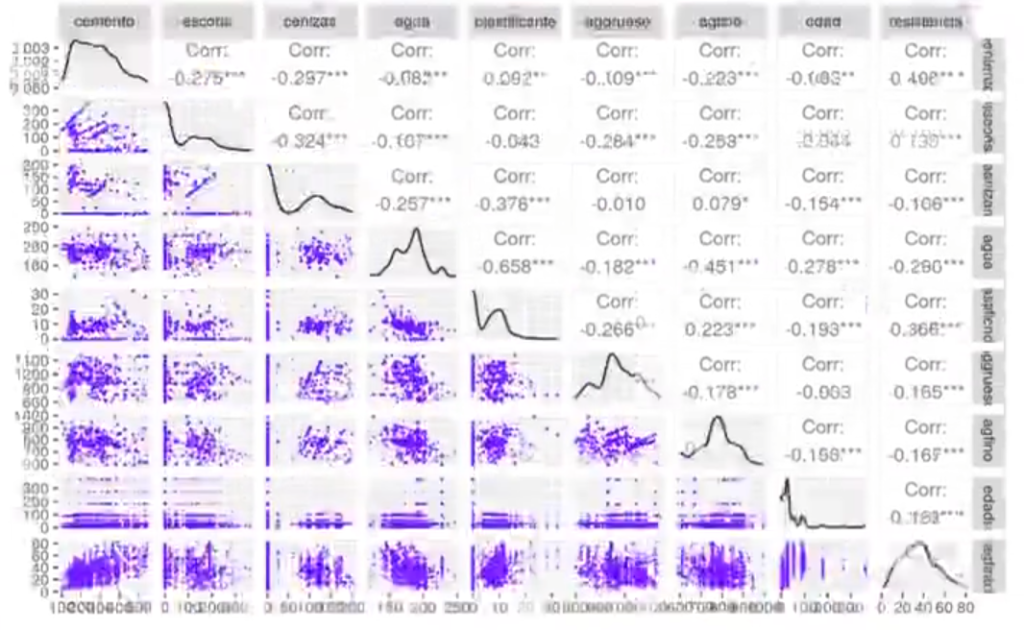
GGally::ggpairs (concrete,
#lower = list (continuous = GGally::wrap ("density", alpha = 0.8, size = 0.2, color = "blue'))
lower = list (continuous = GGally::wrap ("points", alpha = 0.3, size = 0.1, color = "blue'))
)
In [ ] : suppressPackageStartupMessages (library (tidyverse))
suppressPackageStartupMessages (library (glmnetUtils))
In [ ] : set.seed (12)
idx <- sample (1 : nrow (concrete), nrow (concrete) * 0.7)
concrete.train = concrete [idx, ]
concrete.test = concrete [- idx, ]Regresión lineal
In [47] : Im_model <- lm (resistencia ~
cemento * escoria * agua * plastificante * aggrueso * agfino * edad cenizas, data = concrete.train)
Im_yp train <- predict (lm_model, concrete.train) caret::postResample (pred = lm_yp_train, obs = concrete.train$resistencia)
lm_yp_test <- predict (lm_model, concrete.test)
caret::postResample (pred = lm_yp_test, obs = concrete.test$resistencia)Warning message in predict.lm (lm_model, concrete.train):
«prediction from a rank-deficient fit may be misleading»
RMSE: 5.54817427355096
Rsquared: 0.895541903423443
MAE: 4.27848492717393
Warning message in predict.Im (lm_model, concrete.test):
«prediction from a rank-deficient fit may be misleading»
RMSE: 11.6072399677266
Rsquared: 0.610930208024904
MAE: 7.59596108167767
Siguiendo con nuestro ejercicio de regularización en R, en este caso tenemos variables que provienen de diferentes unidades y tienen rangos muy diferentes de valores, por lo que para hacer los coeficientes comparables entre si, deberíamos estandarizarlos.
El resultado consiste en dejar nuestros datos con media O y varianza 1:
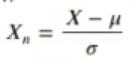
Esto lo realiza por sí solo el paquete gimnet o gimnetutils.
In [48] : cv <- glmnetUtils::cv.glmnet (formula = resistencia ~ cemento * escoria * cenizas * agua * plastificante * aggrueso * agfino * edad, data = concrete.train,
alpha = 1,
nfold = 10,
type.measure = "mse",
standardize = T)
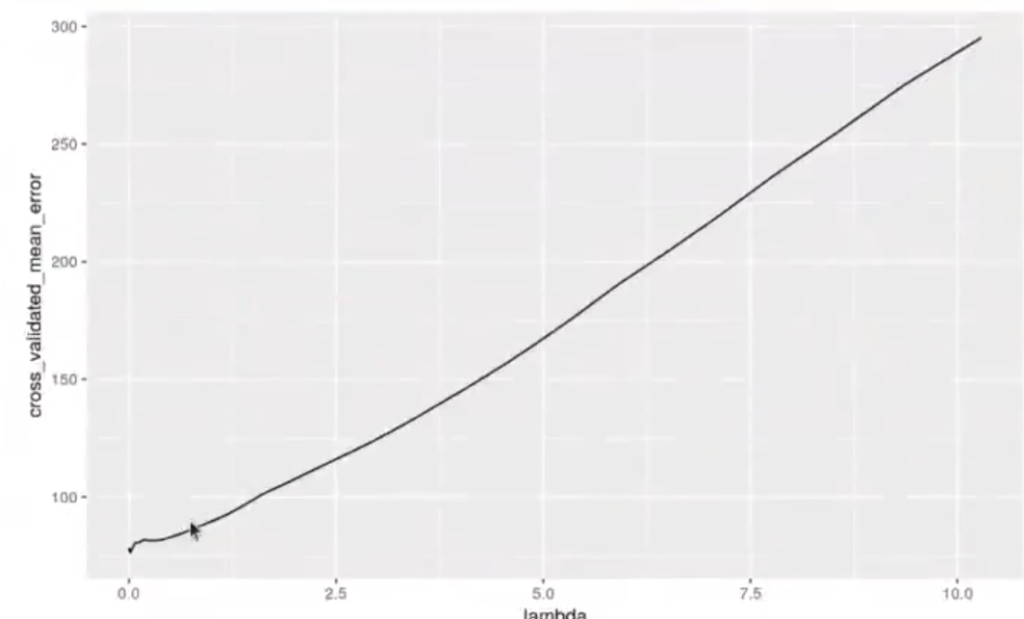
ggplot (data.frame (lambda = cv$lambda, cross_validated_mean_error = cvscvm), aes (x = lambda, y = cross_validated_mean_error)) + geom_line()
paste0 ("El valor lambda con el menor error es:", cvslambda.min)
paste0 ("El valor lambda más alto que se encuentra a una distancia 1sd es:", cvslambda.Ise)
paste0 ("EL R ^ 2 estimado es", cv$glmnet.fit$dev.ratio [which (cv$glmnet.fit$lambda == cv$lambda.lse)])
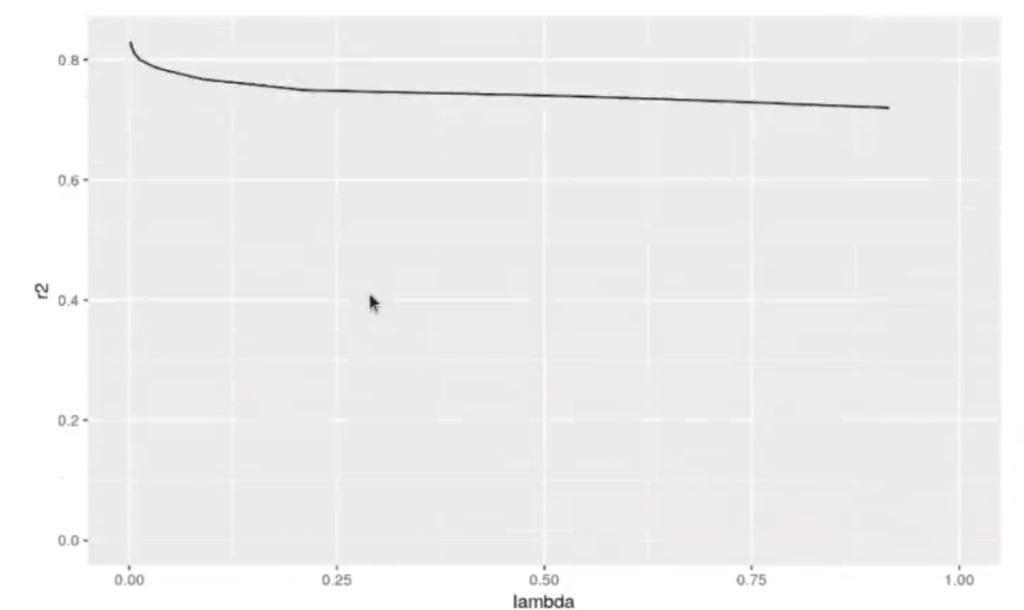
ggplot (data.frame (lambda = cv$lambda, r2 = cv$glmnet.fit$dev.ratio), aes (x = lambda, y = r2)) + geom_line () + xlim (0,1)El valor lambda con el menor error es: 0.0139192431806921
El valor lambda más alto que se encuentra a una distancia 1sd es: 0.524050568773559
El R ^ 2 estimado es: 0.739486340472894
Warning message:
«Removed 26 row (s) containing missing values (geom_path).»
In [49] : reg_yp_train <- predict (cv,
concrete.train,
s = cv$lambda.min)
caret::postResample (reg_yp_train, concrete.train$resistencia)RMSE: 7.68775094434461
Rsquared: 0.799551675780017
MAE: 6.05153325446913
In [50] : reg_yp_test <- predict (cv,
concrete.test,
s = cv$lambda.min)
caret::postResample (reg_yp_test, concrete.test$resistencia)RMSE: 8.36112292024709
Rsquared: 0.708476108521642
MAE:5886841734999
In [ ] : residual test <- concrete.test$resistencia - reg_yp_test
plot (concrete.test$resistencia, residual_test)
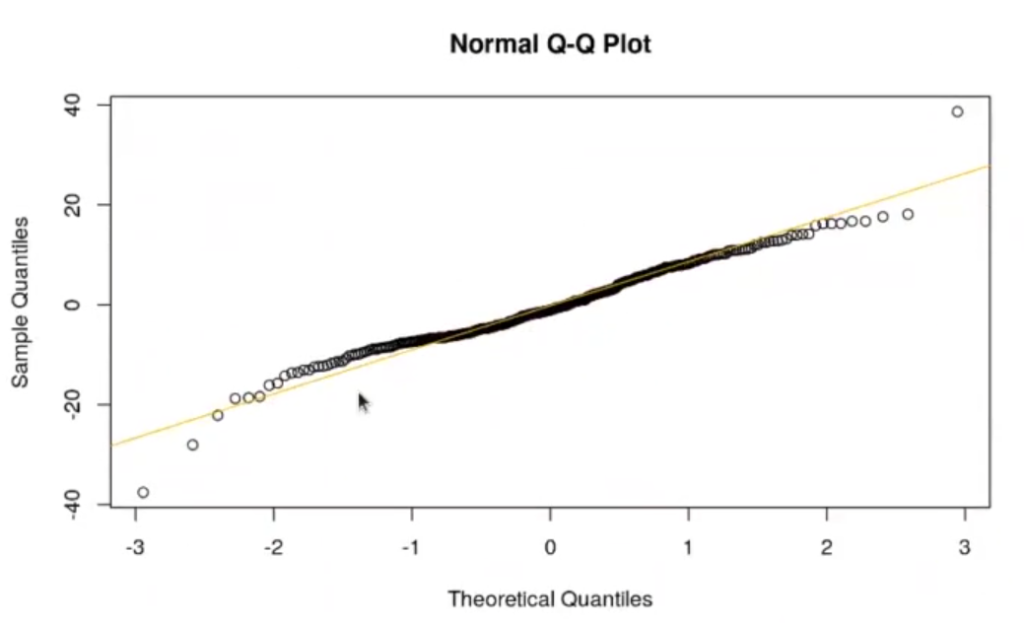
qqnorm (residual test)
qqline (residual_test, col = "orange")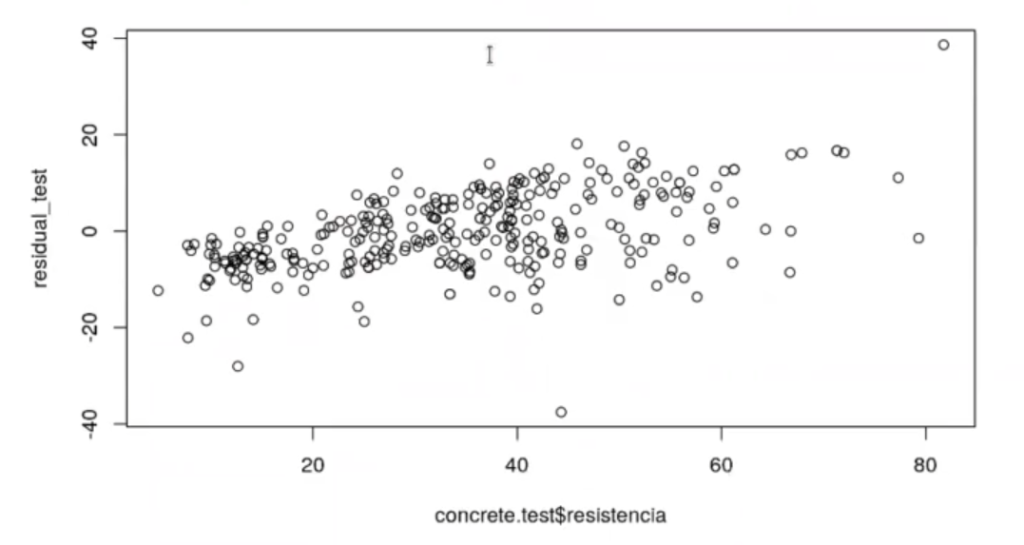
In [52] : data.frame (real = concrete.test$resistencia,
Im = lm_yp_test,
reg = reg_yp_test [ , 1]) %>%
mutate (res_lm = real - lm) %>%
mutate (res_reg = real - reg) -> total_pred
head (total_pred)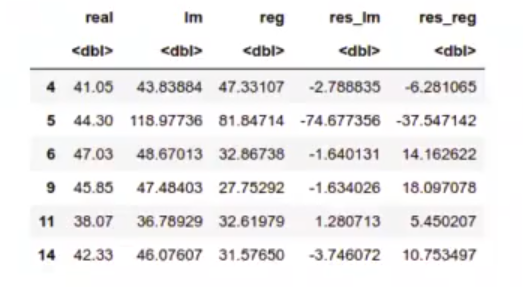
In [ ]: library (reshape2)
total_pred %>% select (res_lm, res_reg) %>% melt()
ggplot (aes (x = value, color = variable)) + geom_density ()
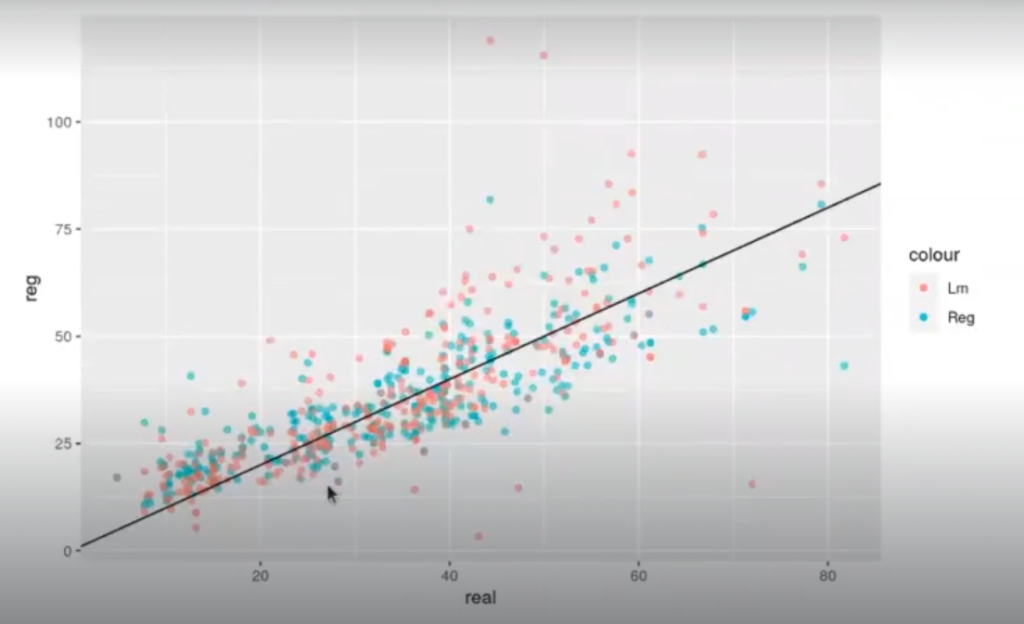
total_pred %>% ggplot (aes (x = real)) +
geom_point (aes (y = reg, color = "Reg"), alpha = 0.5)+
geom point (aes (y = lm, color = "lm"), alpha = 0.5) + geom_abline (intercept = 0, slope = 1)Attaching package: ‘reshape2’
The following object is masked from ‘package:tidyr’:
smiths
No id variables; using all as measure variables
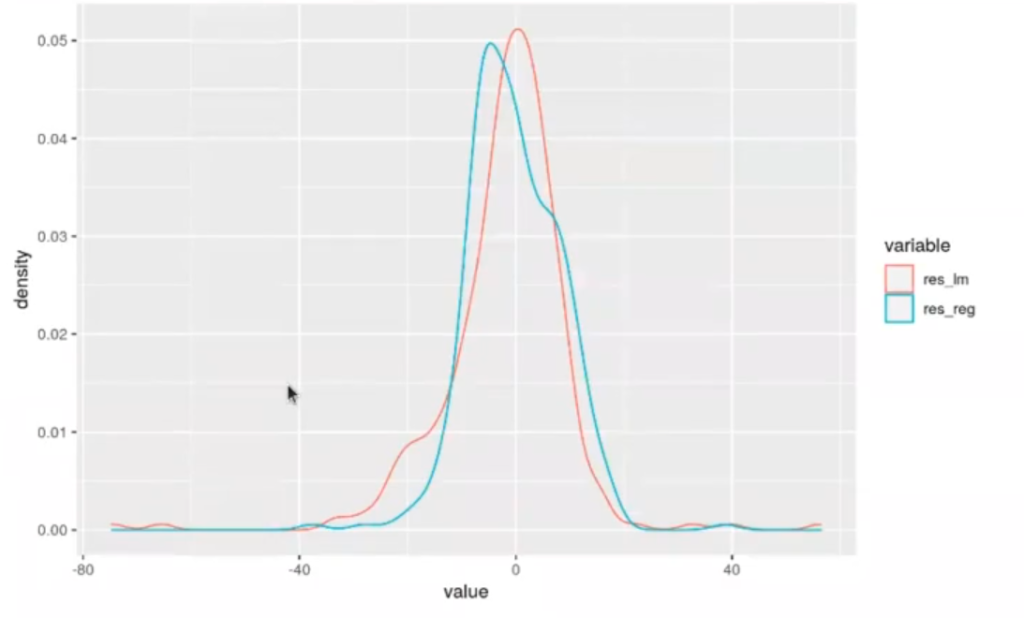
Continuando con el ejercicio de regularización en R, aquí tenemos en testing de cómo serían las distribuciones para el ejercicio de regularización en R y para la lineal.
In [56]: #¿Tiene sesgo nuestro modelo?
colMeans (total_pred [ , c ("res_lm", "res_reg") ] )res_Im: -1.96769345906342
res_reg: -0.125771239962697
Al final, nuestra regularización no tenía sesgos. En este caso, parece que nuestro modelo tiene menos sesgo que el de la regresión lineal, que tenía un poco más. Lo que se hace con este ejercicio de regularización en R es básicamente sumar los residuos de todas las predicciones y observar hacia dónde tiran, es decir, hacia qué lado se inclinan.
¿Te animas a seguir estudiando este tema? Si te has gustado este ejercicio de regularización en R y su respectiva solución, recuerda que puedes encontrar muchos similares y de otros tipos en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, en donde aprenderás en muy poco tiempo a dominar temas relacionados con el Big Data y el data mining, siempre con el acompañamiento de expertos en la materia. Tendrás la oportunidad de acceder a las mejores ofertas laborales de uno de los mercados más prolíficos del momento. ¡No esperes más para inscribirte!











