En este artículo realizaremos un ejercicio práctico de regresión lineal con t-student y ANOVA. El dataset contiene información de bebés recién nacidos y sus madres. Nos vamos a centrar en si la madre era o no fumadora.
¿Qué encontrarás en este post?
ToggleEjercicio práctico de regresión lineal con t-student y ANOVA
In [10]: bwt <- read.csv ("data/birthweight_reduced.csv") bwt$smoker <- factor (bwt$smoker, labels = c ("NO", "YES"))
Repaso t-test
In [11]: tw <- t.test (bwt$Birthweight [bwt$smoker="YES"], bwt$Birthweight [bwt$smoker "NO"])
In [13]: library (ggplot2)
d.f. <- tw$parameter
t <- tw$statistic
loth <- qt (0.025, d.f., lower.tail = T)
upthe <- qt (0.025, d.f., lower.tail = F)
paste ("El margen que nos llevaría a rechazar la hipótesis nula está fuera del rango: [" , round (loth,2), " , " , round(upth, 2),"")
qsd009 <- function (x) {
out <- dt(x, d.f.)
out[x> loth & x<upth] <- NA
out
}
qsdtest <- function (x) {
out <- dt(x, d.f.)
out [x> -abs(t) & x< abs(t)] <- NA
out
}
options (repr.plot.height=4, repr.plot.width=8)
xdf <- data.frame(z=c(-4, 4))
ggplot (xdf, aes (x=z)) + stat function (fun = dt, args = list(df = d.f.))+
stat_function (fun-qsd009, geom = "area", fill = "red", alpha = 0.3)+
stat_function (fun-qsdtest, geom="area", fill="yellow", alpha=0.2)+ geom_text (x = 3, y=0.1, size = 4, label = paste0 ("t_cdf (" , round (upth, 2), ") = 0.975")) + geom_text (x = -3, y = 0.1, size = 4, label = paste ("t_cdf (" ,round (loth, 2), ") = 0.025"))+
geom_vline (xintercept = t, color = "blue")+
theme linedraw ()
options (repr.plot.height = 7, repr.plot.width = 7)
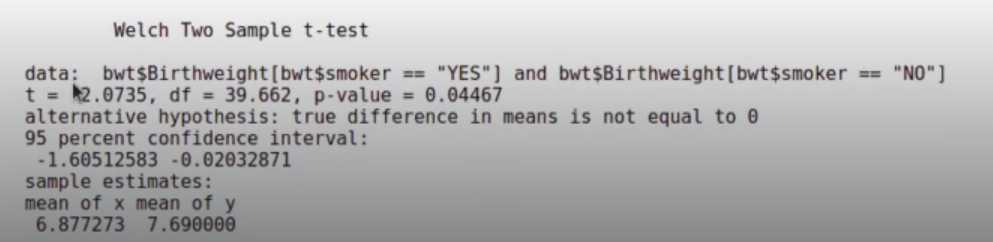
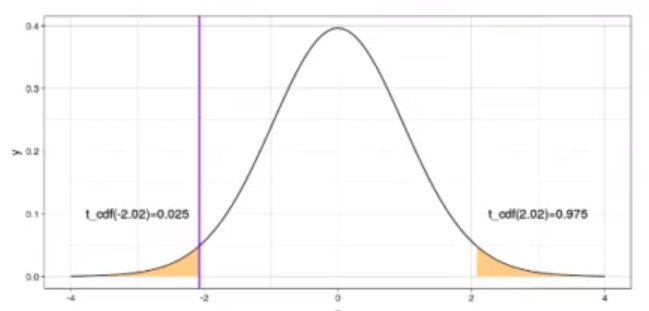
twEl resultado de nuestro ejercicio práctico de regresión lineal con t-student y ANOVA es un test estadístico que es -2.0735. Esto es lo que marca la línea morada en la gráfica siguiente.
‘El margen que nos llevaría a rechazar la hipótesis nula está fuera del rango: [-2.02.2.02]’
¿Qué sabíamos hasta ahora?
Para madres no fumadoras
In [ ] : bwt_nosmoker <- bwt [bwt$smoker = "NO", ]
mn <- mean (bwt_nosmoker$Birthweight)
paste ("La media de peso de los bebes de las madres no fumadoras es de", mn)
paste ("Su desviación típica estimada es de", sd (but_nosmoker$Birthweight))Siguiendo con el ejercicio práctico de regresión lineal con t-student y ANOVA, sabemos que el vector de las medias tiene una distribución gaussiana de media x. Pero en una desviación típica desconocida, estimada a través de la muestra de b/√n, es fácil calcular el intervalo de confianza para la media con una probabilidad de p.
Los intervalos de confianza para un p-valor de p y n muestras vendrá dado por la fórmula:
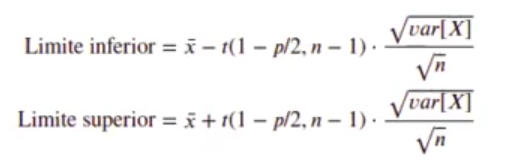
Donde t(pn-1) es la función acumulativa de probabilidad de una distribución t-student con n — 1 grados de libertad.
In [ ] : p <- 0.05
error <- qt (1-p/2, nrow (bwt_nosmoker) -1) * sd (bwt_nosmoker$Birthweight) / sqrt (nrow (bwt_nosmoker))
paste ("El error será: ", error)
paste ("Intervalo de confianza del 95% de la media de no fumadores será: [" , mn-error, " , mn+error, " ] ")Para madres fumadoras
El resultado del ejercicio práctico de regresión lineal con t-student y ANOVA para madres no fumadoras es:
In [16]: bwt_smoker <- bwt [bwt$smoker == "YES", ]
mn_smoker <- mean (bwt_smoker$Birthweight)
paste ("La media de peso de los bebés de las madres fumadoras es de" , mn_smoker)
paste ("Su desviación típica estimada es de " , sd (bwt_smoker$Birthweight))‘La media de peso de los bebés de las madres fumadoras es de 6.87727272727273’
‘Su desviación típica estimada es de 1.3893924051222’
In [17 ]: p <- 0.05
error_smoker <- qt (1 - p/2, nrow (bwt_smoker) - 1) * sd (bwt_smoker$Birthweight) / sqrt (nrow (bwt_smoker))
paste ("El error será: ", error_smoker)
paste ("Intervalo de confianza del 95% de la media de no fumadores será: [" , mn_smoker - error_smoker, " , " , mn_smoker + error_smoker, " ] ")‘El error será: 0.616022081923158’
«Intervalo de confianza del 95% de la media de no fumadores será: [6.26125064534957 , 7.49329480919589]’
In [18] : t.test (bwt_smiker$Birthweight)
In [19]: model <- Im(formula = Birthweight summary (model) smoker, data = bwt)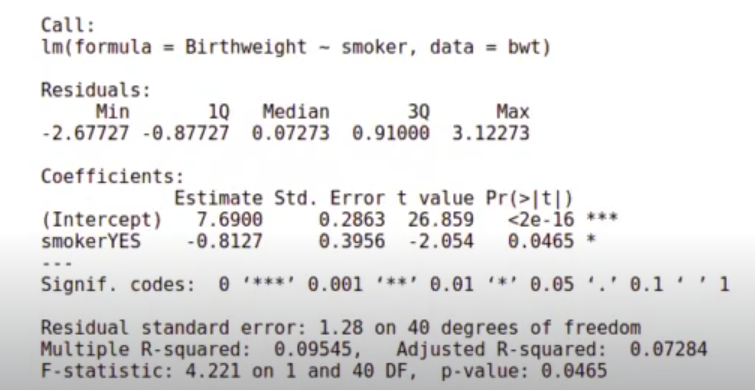
In [20]: paste("La media de peso de los bebés de las madres NO fumadoras es de", model$coefficients[1]) paste("La media de peso de los bebés de las madres fumadoras es de", model$coefficients [1]+model$coefficients[2])‘La media de peso de los bebés de las madres NO fumadoras es de 7.69’
‘La media de peso de los bebés de las madres fumadoras es de 6.87727272727273’
El siguiente paso en el ejercicio práctico de regresión lineal con t-student y ANOVA es ver cuál es el peso de los niños de madres fumadoras y no fumadoras. Podríamos hacer lo siguiente:

Ahora, siguiendo con nuestro ejercicio práctico de regresión lineal con t-student y ANOVA, calcularemos los márgenes de confianza:
| 2.5 % | 97.5 % | |
| smokerNO | 7.111355 | 8.26864 |
| smokerYES | 6.325557 | 7.428989 |
No podemos estar muy seguros de si fumar o no es malo, solo con este modelo, de ahí la necesidad de calcular los márgenes de confianza.
Como hemos con el margen de confianza, el resultado de nuestro ejercicio práctico de regresión lineal con t-student y ANOVA es bastante claro y preciso.
Recuerda que, si quieres seguir aprendiendo sobre estas temáticas y otras tantas, puedes seguir nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el cual en muy poco tiempo podrás incursionar en el mercado laboral más prolífico de la actualidad y ser un gran profesional. ¡No esperes más para inscribirte y sigue forjando tu futuro con nosotros!











