Un estimador en estadística Big Data forma parte de la cantidad de estrategias que tratan de entender las variables y las relaciones que se pueden producir entre ellas. De esta manera, podrás comprender cómo funciona la población de datos que te encuentras procesando.
Por esta razón, la implementación de un estimador para un estudio de datos estadístico resulta imprescindible; en efecto, debes aprender no solo qué es, sino para qué sirve dentro del mundo del manejo de los macrodatos. En este post, te explicamos qué es un estimador en estadística Big Data y cuáles son sus principales tipos según las funciones que desempeña.
¿Qué es un estimador en estadística Big Data?
Un estimador en estadística Big Data posee una serie de variantes según la estrategia utilizada para llevar a cabo un análisis estadístico de los macrodatos. Su principal característica radica en que es un estadístico (esto es, una función de la muestra) usado para estimar un parámetro desconocido de la población, de manera que se presenta como una función que sustrae valores de una muestra de datos y hace un resumen, estima un valor que define la muestra.
Ahora, según la forma en la que estudia los datos, un estimador en estadística Big Data posee diferentes tipos según las funciones que implica. A continuación, te compartimos cuáles son sus principales tipos a partir del siguiente ejemplo:
alturas<-c (1.80,1.60,1.50,1.90,1.75,1.63,1.65)
Media aritmética
En matemáticas y estadística, la media aritmética (también llamada promedio o media) de un conjunto finito de números es el valor característico de una serie de datos cuantitativos, objeto de estudio que parte del principio de la esperanza matemática o valor esperado. Se obtiene a partir de la suma de todos sus valores dividida entre el número de sumandos:
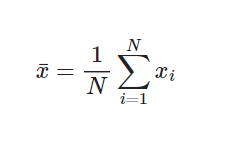
En R, la función de la media se podría definir así:
myMean<-function(X){
# A rellenar
}
myMean(alturas)
Evidentemente, R tiene una función para la media cuya ejecución es mucho más rápida que la función:
mean(alturas)
Varianza/desviación típica
La variancia, que suele representarse como σ², s² o Var(X), de una variable aleatoria es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media. En otras palabras, es la media de los residuos al cuadrado.
Es decir, define lo mucho que varía una variable aleatoria respecto a la media:
- Si todos los valores son iguales, no hay variación, entonces la varianza es 0.
- Si los valores son muy diferentes unos de otros, la varianza es alta.
El motivo de usar el cuadrado es porque se quiere ver lo mucho que cambia cada elemento sin importar su signo, si cambia por arriba o por abajo, el signo se elimina. El hecho de ser una función al cuadrado también da mayor importancia a los valores extremos. El problema que esto origina es que las unidades de la varianza están también al cuadrado, por ello, a veces se utiliza la desviación típica.
La raíz cuadrada de la varianza es la desviación típica que indica cómo de típica es dicha desviación respecto a la media en sus mismas unidades.
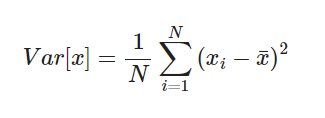
Mediana
La mediana es el valor de una distribución donde la mitad de los elementos son superiores y la mitad son inferiores.
myMedian<-function(x){
# A rellenar
}
myMedian(alturas)
Por otra parte, la media y la mediana no tienen que ser iguales. Por ejemplo, salarios brutos españoles de 2016:
- Salario medio: 1878,1€/mes.
- Salario mediano: 1594,5€/mes.
Esto indica que hay poca gente con sueldos muy altos que sube la media, la distribución no es simétrica.
Cuartiles
Los cuartiles son los tres valores que dividen un conjunto de datos ordenados en cuatro partes porcentualmente iguales.
- Q1: El 25% de las muestras se encuentran por debajo del primer cuartil.
- Q2: El 50% de las muestras se encuentran por debajo del segundo cuartil. Este valor también se conoce como mediana.
- Q3: El 75% de las muestras se encuentran por debajo del tercer cuartil.
- Rango intercuartílico (IQR): Q3-Q1.
Una forma muy práctica de mostrar estos valores es con el diagrama de cajas (boxplot en inglés). El boxplot se compone de:
- Caja (box): el lado superior indica el lugar de Q3, el lado inferior es Q1 y la línea que lo atraviesa es Q2.
- Bigotes (whiskers): dos líneas que se extienden 1.5 veces el IQR desde Q3 y desde Q1.
- Valores atípicos (outlayers): valores que se encuentran fuera de los bigotes.
¿Cómo aprender más sobre los estimadores en estadística Big Data?
En este post, te hemos explicado qué es un estimador en estadística Big Data y cuáles son sus principales tipos para implementarlo en un estudio estadístico de los macrodatos según su función e interés.
Si aún deseas aprender más sobre el Big Data, desde KeepCoding te traemos el Bootcamp Full Stack Big Data, Inteligencia Artificial & Machine Learning, en el que se exponen los sistemas y herramientas más importantes en el universo del Big Data. ¡No dudes en solicitar más información e inscríbete ahora!











