Los estimadores de máxima verosimilitud (EMV) o maximum likelihood estimation (MLE) son diferentes en los modelos Bernoulli y binomial.
Esto sucede por la forma en la que se han optimizado dichas ecuaciones. Estamos optimizando algo que, conceptualmente, tiene una forma distinta, pero al final tiende al mismo punto.
¿Qué encontrarás en este post?
Toggle¿Qué son los estimadores de máxima verosimilitud?
La estimación de máxima verosimilitud es uno de los métodos numéricos que se usa para determinar valores para los parámetros de una distribución.
Modelo Bernoulli
Para evaluar los estimadores de máxima verosimilitud, se tratará de modificar los valores de β para que la siguiente función sea máxima:
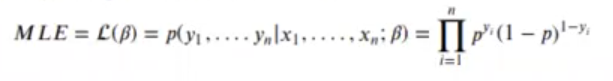
Para simplificar pasamos a logaritmos:
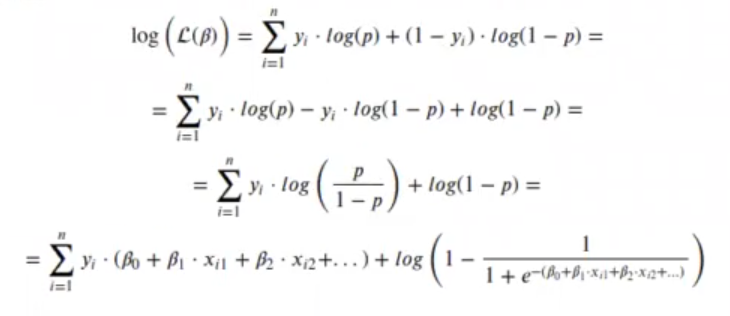
Binomial
Para evaluar los estimadores de máxima verosimilitud, se tratará de modificar los valores de β para que la siguiente función sea máxima:
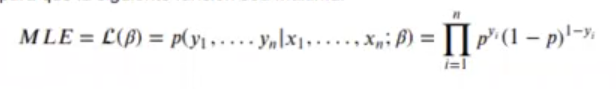
Para simplificar pasamos a logaritmos:
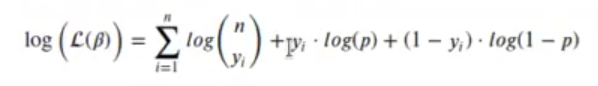
Un ejemplo de estimadores de máxima verosimilitud
Vamos a generar una secuencia de valores de x que podrían ser 0.2, 0.4 y 0.1:
In [29] : set.seed (123)
x <- rep (c (rep (0.2, 3), rep (0.4, 2), rep (0.1, 6)), 10)
y <- sapply (x, function (xi) rbinom (1, size = 1, prob = xi * 2 + 0.1))
df <- data.frame (y, x)
df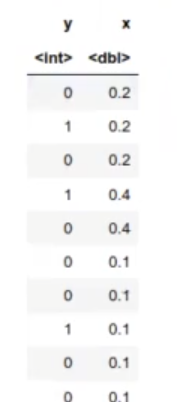
A cada uno de esos valores (0.2, 0.4 y 0.1) se le asignará un valor Y de 0 o de 1 (tal y como se muestra en la imagen).
¿Cómo están relacionados los valores de X e Y? Por medio del rbinom. Al rbinom se le daba una función aleatoria binomial:
In [30] : rbinom (1, size = 1, prob = 0)0
Siguiendo con el ejercicio de estimadores de máxima verosimilitud, si le decimos que solo saque una muestra, que el tamaño (size) es 1, y tenemos una distribución binomial donde solo estamos tirando una moneda, por ejemplo (y no 3), es una Bernoulli. Si estuviéramos tirando 3 monedas, por ejemplo, sería una binomial pura.
El código anterior lo que hace es devolver una cara o una cruz, en función de la probabilidad que le decimos. Si ponemos una probabilidad de 0, nunca va a salir cruz. Si en prob ponemos 0.2, el 20% de las veces va a salir cara, es decir, va a salir 1.
In [30] : rbinom (1, size = 1, prob = 0.2)Si le ponemos 0.9, va a haber un 90% de probabilidades de que salga 1:
In [30] : rbinom (1, size = 1, prob = 0.9)Aquí no estamos diciendo que la probabilidad sea constante. Todo lo contrario, la probabilidad va a depender del valor de X.
Estamos, pues, trabajando con el valor de X, que puede ser cualquier valor de los mostrados en la imagen de resultados de la ecuación. A continuación, el resumen de la tabla de estimadores de máxima verosimilitud:

Si nos fijamos en la ecuación para generar la secuencia de valores, podemos comprobar la validez de estos cálculos que nos ha arrojado la matriz:
y <- sapply (x, function (xi) rbinom (1, size = 1, prob = xi * 2 + 0.1))Aquí reemplazamos xi por cualquiera de los tres valores propuestos:
0.4 * 2 = 0.8
0.8 + 0.1 = 0.9
Como vemos, las probabilidades encajan con el resultado mostrado en la tabla. Lo mismo pasa si reemplazamos el valor de xi por cualquiera de los otros dos valores restantes. Hagámoslo con 0.1:
0.1 * 2 = 0.3
0.2 + 0.1 = 0.3
Podríamos hacer los cálculos a mano, de modo que:
18 / 20 = 0.9 : esta sería la probabilidad para 0.4
15 / 30 = 0.5
16 / (44+16) = 2.6666666
o
0.1 * 2 + 0.1 = 0.3
Todos estos cálculos de estimadores de máxima verosimilitud que hemos hecho a mano pueden hacerse calculando una regresión:
In [109]: model_bernoulli <- gla (data = df, formula = y ~ x, family = binomial)
Summary (model_bernoulli)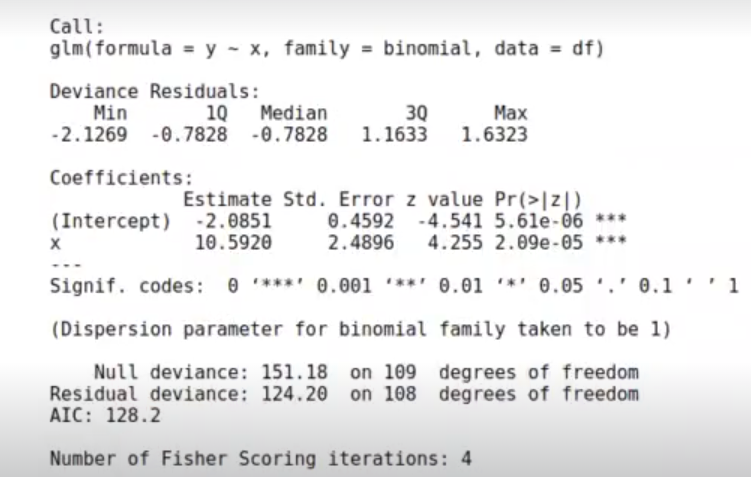
Calculemos unos valores de X que vayan desde 0 hasta 0.4, que es el valor máximo:
In []: options (repr.plot.height = 4, repr.plot.width = 6, repr.plot.res = 200)
x_lin <- seq (0, 0.4, length.out = 20)
prob_real <- x_lin * 2 + 0.1
log_odds_real <- log (prob_real / (1 - prob_real))
plot (x_lin, log_odds_real, t = 'l')
log_odds_est <- model_bernoulli$coefficient [1] + model_bernoulliscoefficient [2] * x_lin
#log_odds_est <- predict (model_bernoulli, data. frame (x = x_lin))
lines (x_lin, log_odds_est, col = "red")Hemos cogido un valor de x que va de 0 a 0.4 y debajo se ha puesto la probabilidad real. Luego hemos pintado el logaritmo de la razón de momios de la probabilidad real. Al resultado de esta operación le hemos aplicado el logaritmo natural.
Posteriormente, lo pintamos. Lo que vamos a pintar es el resultado de la regresión, los coeficientes del logaritmo de la razón de momios. Vamos a ver cómo queda:
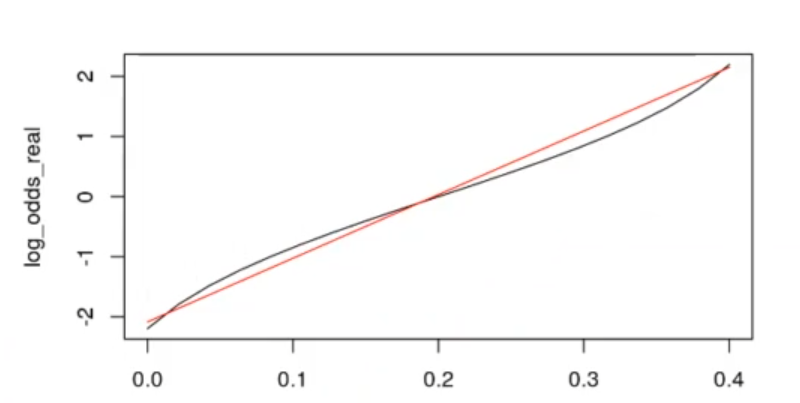
En rojo está la línea que estamos prediciendo; en negro, la curva real.
Esta gráfica podríamos modificarla para que ambas líneas quedaran rectas y la probabilidad fuera más precisa.
Sabemos que esto de los estimadores de máxima verosimilitud puede ser difícil. Por ello, te invitamos a inscribirte en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, la formación intensiva e íntegra con la que, en unos pocos meses, estarás más que capacitado para incursionar en el mercado laboral IT. ¡Anímate a solicitar información!











