Cuando empecé a trabajar con grandes volúmenes de datos en entornos de Big Data, una de las herramientas que más revolucionó mi forma de pensar fue la función de densidad de probabilidad. No se trata solo de una fórmula matemática; es una puerta para entender cómo se comportan los fenómenos reales en el mundo de la estadística.
Si quieres comprender cómo se distribuyen los datos continuos y cómo puedes estimar probabilidades dentro de intervalos específicos, esta guía es para ti.
¿Qué es la función de densidad de probabilidad?
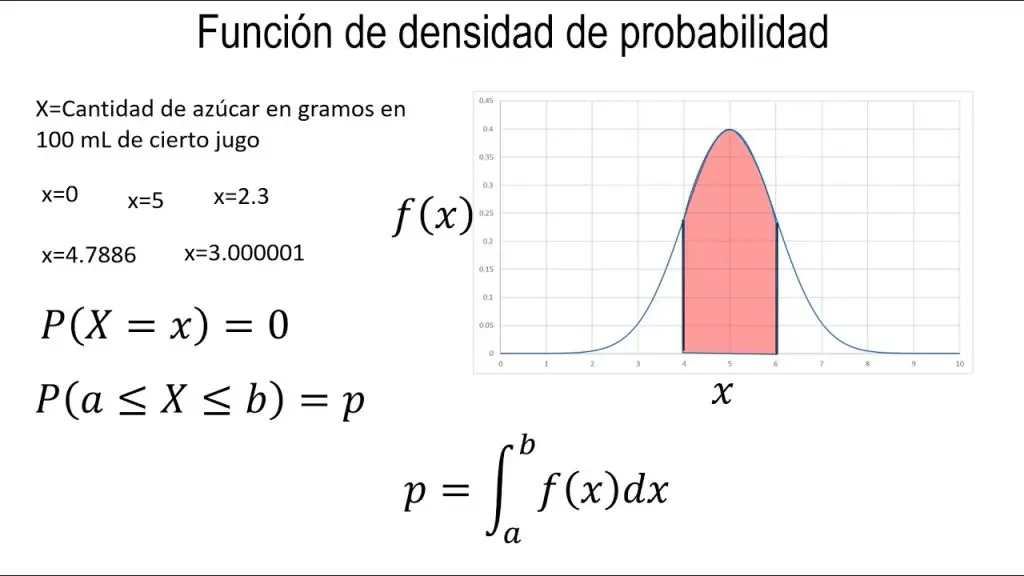
La función de densidad de probabilidad (FDP) es una herramienta estadística que describe la probabilidad de que una variable aleatoria continua tome un valor dentro de un intervalo determinado. A diferencia de las variables discretas, donde se asignan probabilidades exactas a ciertos valores, en el caso de variables continuas, la probabilidad de que el valor sea exactamente uno es cero.
En cambio, calculamos la probabilidad de que la variable se sitúe entre dos puntos, lo que se representa mediante la integral de la función de densidad en ese rango.

Propiedades de la función de densidad de probabilidad
Para comprender sus propiedades, supongamos que f(x) es la función de densidad de probabilidad de una variable aleatoria continua x. Su integral a lo largo de todo el dominio debe ser igual a 1. Es decir, la suma de todas las probabilidades posibles es del 100%.
- No negatividad: Para cualquier valor de x, f(x) ≥ 0.
- Área total bajo la curva = 1: ∫ f(x) dx sobre todo el dominio = 1.
- Probabilidad entre dos valores: P(a ≤ X ≤ b) = ∫ₐᵇ f(x) dx.
Fórmulas según el tipo de variable
- Para variables continuas: P(a≤X≤b)=∫abf(x)dxP(a ≤ X ≤ b) = \int_a^b f(x) dxP(a≤X≤b)=∫abf(x)dx
- Para variables discretas, aunque no se hable estrictamente de densidad, se utiliza la función de masa de probabilidad: P(X=x)=f(x)P(X = x) = f(x)P(X=x)=f(x)
Ejemplo práctico: ¿Cuál es la probabilidad de que alguien al azar en España sea milenial?
Tomando datos de distribución por edad en España, se puede calcular la probabilidad de que una persona elegida aleatoriamente haya nacido entre 1980 y 2000 (considerados milenials).
Este es un ejemplo realista de cómo usamos funciones de densidad y proporciones en análisis demográfico:
f_poblacion <- poblacion[,c("Total","edad")]
f_poblacion$nacimiento <- 2021 - f_poblacion$edad
f_poblacion$Ratio <- f_poblacion$Total / sum(f_poblacion$Total)
f_poblacion_milenial <- sum(f_poblacion$Ratio[
f_poblacion$nacimiento >= 1980 & f_poblacion$nacimiento <= 2000
])
paste("La probabilidad de que eligiendo una persona al azar en España sea milenial es ",
f_poblacion_milenial)
Resultado: La probabilidad calculada es de aproximadamente 0.25036, es decir, un 25%.
Aplicaciones reales
La función de densidad de probabilidad es esencial en muchos sectores:
- Big Data: para modelar patrones de consumo, comportamiento o riesgos.
- Finanzas: al evaluar probabilidades de pérdida o ganancia en mercados volátiles.
- Ciencia de datos e IA: en modelos de regresión, clasificación y redes bayesianas.
- Ingeniería: en control de calidad y análisis de confiabilidad.
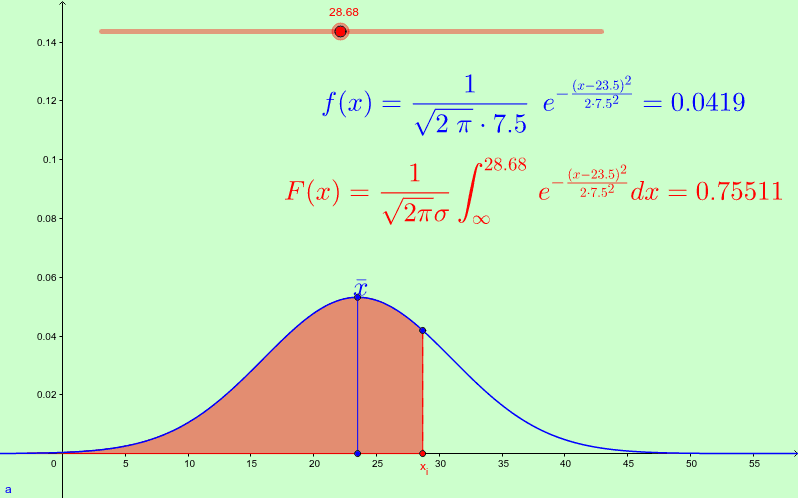
¿Y qué hay de la función de densidad condicional?
Este tipo de función (la función de densidad condicional), que hemos tratado en profundidad en otro artículo, permite calcular probabilidades condicionadas a que otra variable haya tomado cierto valor. Es vital en estadística bayesiana y modelos predictivos más avanzados.
Conclusión sobre la función de densidad de probabilidad
La función de densidad de probabilidad te permite ir más allá de simples estadísticas descriptivas. Te da una mirada profunda y estructurada sobre cómo se comportan los datos en el mundo real. Si trabajas con grandes volúmenes de información o quieres mejorar tus capacidades de modelado, dominar esta herramienta es imprescindible.
¿Quieres seguir avanzando y dominar técnicas estadísticas, lenguajes de programación como Python y herramientas de análisis de datos en la nube? En el Bootcamp Big Data y Data Science aprenderás a construir sistemas robustos, escalables y preparados para el análisis avanzado de datos. Es la formación perfecta para quienes desean combinar estadística, programación y arquitectura cloud en un perfil profesional único y altamente demandado.











