Las matemáticas para el aprendizaje automático son los conceptos álgebra lineal, cálculo, probabilidad y estadística que te permiten entender, entrenar y evaluar modelos de ML de forma clara y correcta.
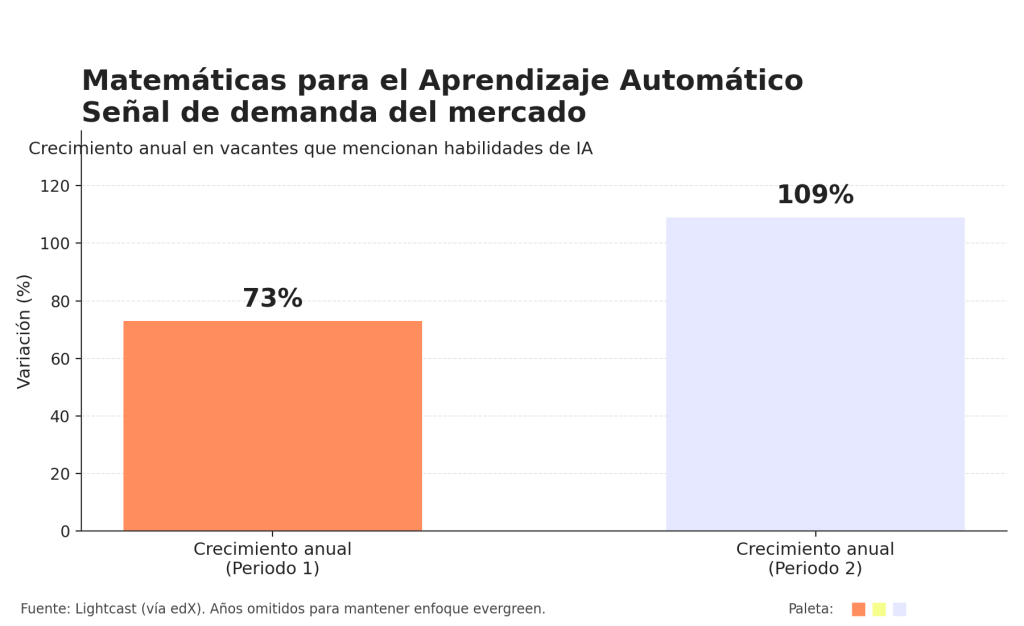
Según datos de Lightcast vía edX, las vacantes que mencionan habilidades de IA crecieron +73% y luego +109%, señalando una demanda acelerada; y el BLS indica que para roles como Data Scientist suele requerirse formación en matemáticas/estadística/CS y reporta una mediana salarial anual de $112,590 (EE. UU.), reforzando que dominar estas bases matemáticas es una ventaja directa para entrar y rendir en ML.
Cuando inicié mi carrera en inteligencia artificial, me di cuenta pronto de que el aprendizaje automático no se trata solo de programar o entrenar modelos con datos. En el centro de esta disciplina están las matemáticas para el aprendizaje automático, la herramienta invisible que da estructura y rigor a cada algoritmo que utilizamos. En este artículo quiero compartir contigo cuáles son esas matemáticas fundamentales, por qué importan realmente, y cómo puedes abordarlas con un enfoque práctico para transformar tu forma de trabajar en machine learning.
¿Por qué las matemáticas para el aprendizaje automático son imprescindibles?
El aprendizaje automático depende de modelos matemáticos que capturan patrones en datos complejos. Sin una base sólida en matemáticas, muchas veces cometemos errores sutiles que limitan el rendimiento o, peor aún, confiamos en resultados sin entender sus fundamentos. Por ejemplo, recuerdo un proyecto donde establecimos un modelo de regresión para predecir ventas, pero sin comprender bien el cálculo del gradiente descendente, el modelo nunca convergió adecuadamente. Sólo tras revisar la derivación de funciones de coste y ajustar los parámetros manualmente, pudimos obtener resultados fiables. Esto demuestra que dominar las matemáticas no es un lujo, sino una necesidad.
Las áreas matemáticas que más impactan en el aprendizaje automático son:
- Álgebra lineal
- Cálculo diferencial e integral
- Probabilidad y estadística
- Teoría de la optimización
Cada una aporta desde la representación del dato hasta la mejora iterativa del modelo.
1. Álgebra lineal: la estructura sobre la que se levantan los modelos
Gestionar grandes volúmenes de datos requiere operar con vectores y matrices. Desde relaciones entre características hasta transformaciones en redes neuronales, el álgebra lineal es la base. Por ejemplo, las redes neuronales convolucionales usan multiplicaciones matriciales para procesar imágenes. Si dominas conceptos como espacios vectoriales, normas, productos escalares y descomposiciones matriciales, podrás entender mejor las implementaciones y optimizaciones en frameworks como TensorFlow o PyTorch.
2. Cálculo diferencial e integral: el motor que impulsa la optimización
Cuando los algoritmos ajustan parámetros para minimizar el error, lo hacen a través de técnicas de cálculo, especialmente derivadas y gradientes. El descenso del gradiente, que actualiza parámetros con base en la pendiente de la función de coste, es un ejemplo clásico. Comprender cómo se calculan derivadas parciales y gradientes, así como conceptos de optimización convexa, es fundamental para diseñar modelos que converjan rápido y eviten problemas como caer en mínimos locales.
3. Probabilidad y estadística: modelando la incertidumbre real
Los datos nunca son perfectos ni exactos. La probabilidad nos ayuda a modelar la incertidumbre y la variabilidad de los datos, mientras que la estadística permite inferir patrones con fundamentos sólidos.
Temas como variables aleatorias, distribuciones, normal, binomial, etc., estimación puntual y por intervalos, y pruebas de hipótesis, son claves para evaluar la confiabilidad de un modelo. En tareas como clasificación o detección de anomalías, sin estas herramientas, cualquier resultado queda en el terreno de las suposiciones.
4. Teoría de la optimización: buscando las mejores soluciones
Al elegir los parámetros que hacen mejor nuestro modelo, nos enfrentamos a problemas complejos que requieren métodos de optimización. Desde algoritmos básicos como el descenso de gradiente hasta técnicas avanzadas como optimización estocástica o algoritmos genéticos, el conocimiento en esta área ayuda a encontrar soluciones eficientes y escalables. Recordemos que el desafío no es solo encontrar un buen resultado, sino hacerlo con rapidez y estabilidad.
Cómo integrar y aprender las matemáticas para el aprendizaje automático

A lo largo de mis años formando profesionales, he comprobado que el mejor aprendizaje surge cuando combinamos teoría con aplicación práctica. Aquí algunas recomendaciones:
- Aprende con cursos especializados: Plataformas como Coursera o edX ofrecen cursos diseñados específicamente para matemáticas en machine learning. Busca que incluyan ejercicios prácticos y proyectos para consolidar conceptos.
- Estudia libros con enfoque aplicado: Mathematics for Machine Learning de Deisenroth, Faisal y Ong es excelente para entender los fundamentos desde cero hasta niveles intermedios.
- Trabaja en proyectos reales: No hay mejor forma de aprender que aplicando los conceptos matemáticos en datasets reales, como los disponibles en Kaggle.
- Desglosa problemas complejos en pequeños bloques: Si una fórmula o concepto parece duro, intenta implementarlo paso a paso, visualizando resultados.
- Forma parte de comunidades técnicas: Interactuar con otros aprendices ayuda a resolver dudas y a recibir feedback.
Un ejemplo práctico: la regresión lineal desde cero
Para entender mejor estas matemáticas, te comparto cómo implementé una regresión lineal simple en Python, sin librerías avanzadas, para predecir la temperatura de un día según horas de sol. Calcule los coeficientes minimizando la suma de los errores cuadrados, aplicando cálculo diferencial para encontrar la derivada de la función de pérdida y ajustando los parámetros con descenso de gradiente. Este ejercicio me ayudó a comprender de primera mano la integración de álgebra lineal y cálculo. Si alguna vez te has sentido intimidado por tanta teoría, mi consejo es comenzar con problemas así antes de pasar a modelos más complejos.
Enlace con KeepCoding para avanzar en tu formación
En KeepCoding, ofrecen el Bootcamp Big Data, Data Science, ML & IA Full Stack que profundiza en estos temas, combinando teoría y práctica en proyectos reales. Esta formación es ideal si quieres dar un salto profesional y dominar realmente el aprendizaje automático desde sus cimientos matemáticos.

Si quieres transformar tu futuro profesional y sumergirte en las matemáticas para el aprendizaje automático con una experiencia completa y enriquecedora, te invito a conocer este Bootcamp. En la búsqueda de contenido aún más detallado sobre las bases matemáticas del aprendizaje automático, te recomiendo consultar la obra de Khan Academy sobre Álgebra lineal y Cálculo, disponible en este enlace.











