En este artículo veremos en qué consiste la métrica en clasificación de la curva ROC y cómo podemos sacar el mayor provecho. Recordemos que la sigla ROC quiere decir Receiver Operating Characteristic, lo que se puede traducir como Característica Operativa del Receptor.
¿Cómo funciona la métrica en clasificación de la curva ROC?
Existen diferentes métricas que nos pueden ayudar con un problema de clasificación binaria. Si tenemos un modelo de clasificación que presenta inconvenientes, podemos utilizar diferentes métricas, como las tasas de interés, directamente relacionadas con la matriz de confusión.
Asimismo, podemos emplear la métrica en clasificación de la curva ROC, que representa la sensibilidad versus uno menos la especificidad o tasa de falso positivo cuando vamos desplazando el umbral. Esto se puede traducir en la siguiente ecuación:
SEN vs 1 – ESP
Veamos cómo funciona esta métrica en clasificación de la curva ROC:
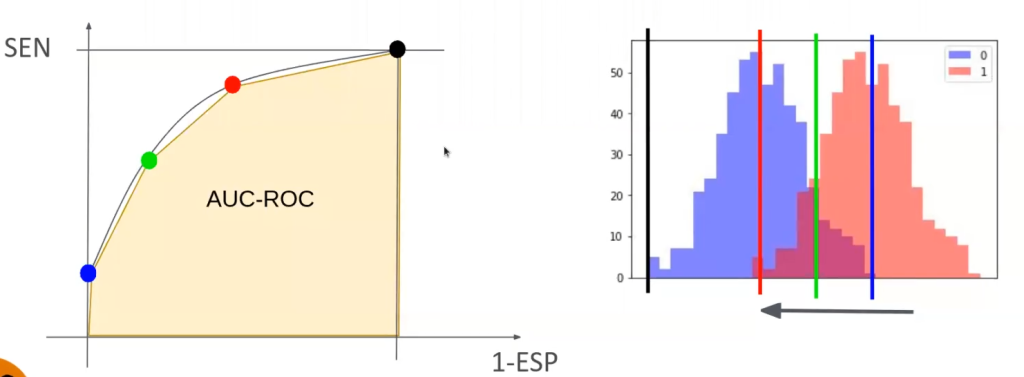
Vamos a partir de un punto, que en nuestro caso es el punto azul. Vamos a ir moviéndonos hacia arriba, uniendo cada uno de los puntos (azul, verde, rojo y negro) y con esto formamos la curva ROC.
Si calculamos el área debajo de la curva (señalada con color amarillo pastel), esto es lo que se denomina como AUC o AUC – ROC y quiere decir area under the curve.
En la métrica en clasificación de la curva ROC, dicha curva se traza con TPR contra FPR; TPR está en el eje y y FPR en el eje x. TPR es la sigla asignada para True Positive Rate y, en contraposición, FPR es la sigla asignada para False Positive Rate.
TP
TPR / Recall / Sensitivity = —————
TP + FN
AUC – Area Under Curve
AUC se traduce como área bajo la curva, porque es el espacio que se puede medir por debajo de la curva que se forma.
El área bajo la curva es medible porque representa un espacio bidimensional completo que evalúa el rendimiento en los problemas de la métrica en clasificación de la curva ROC.
Para que sea más entendible, mirémoslo del siguiente modo: la curva ROC es una curva de probabilidad y el AUC representa el grado o medida de separabilidad, es decir, nos dice lo capaz que es nuestro modelo de distinguir entre sus diferentes clases.
Cuanto mayor es el AUC, mejor será el modelo para predecir 0 clases como 0 y 1 clases como 1.
Con el AUC de la métrica en clasificación de la curva ROC seguimos trabajando solo para resolver problemas binarios, de ahí que siempre se haga una analogía muy simple: cuanto mayor sea el AUC, mejor será el modelo para distinguir entre pacientes infectados y no infectados.
Situación ideal de la métrica en clasificación de la curva ROC
La situación ideal de la métrica en clasificación de la curva ROC estaría dada por la completa separabilidad. Esta situación ideal nos permitiría tener un error cero.
En cuanto al área bajo la curva, el mejor caso posible es que AUC – ROC = 1. Veamos:
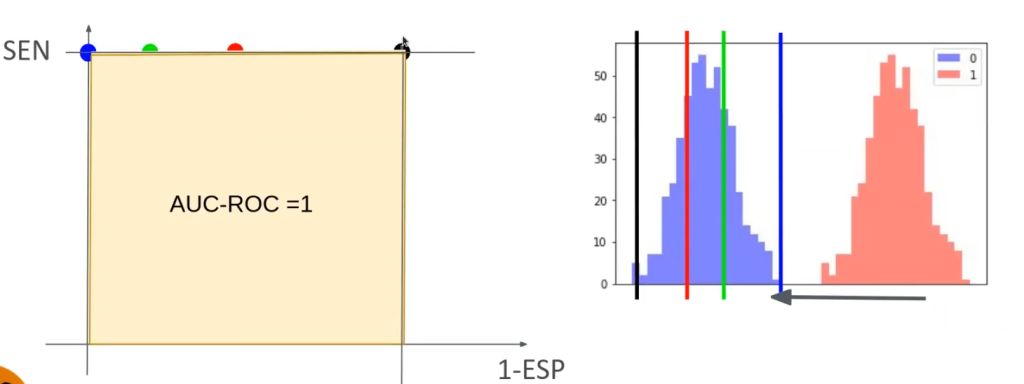
En el otro lado del espectro, el peor caso posible sería que todo estuviera superpuesto:
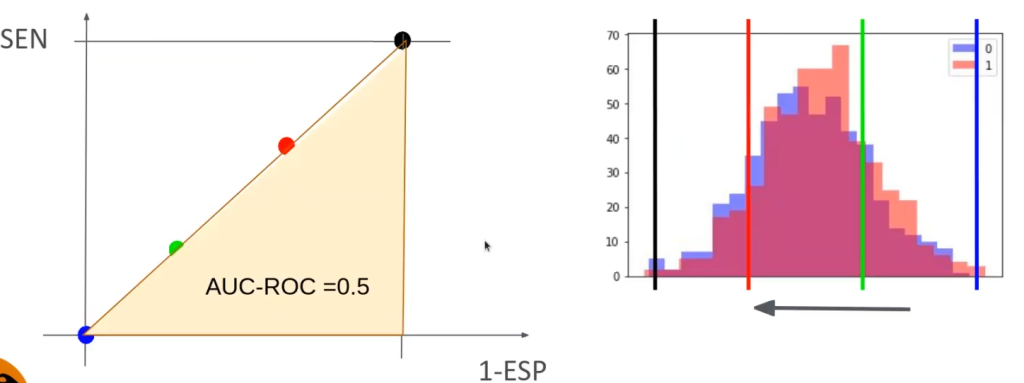
Utilidad de la métrica en clasificación de la curva ROC
Una de las grandes utilidades que tiene la curva ROC es que es un método muy interesante para comparar clasificadores. Hay que intentar aproximarse lo máximo posible a la esquina superior izquierda.
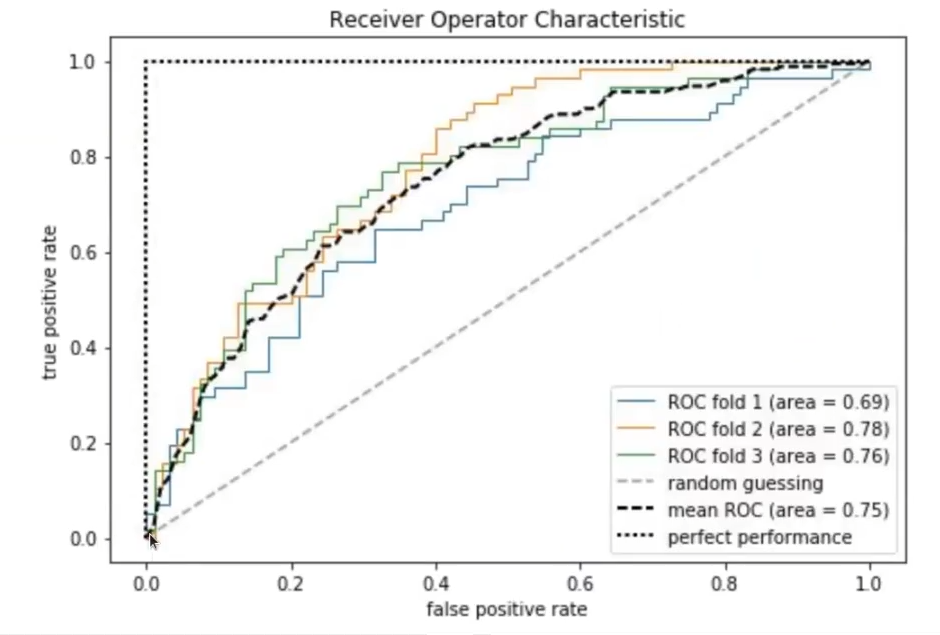
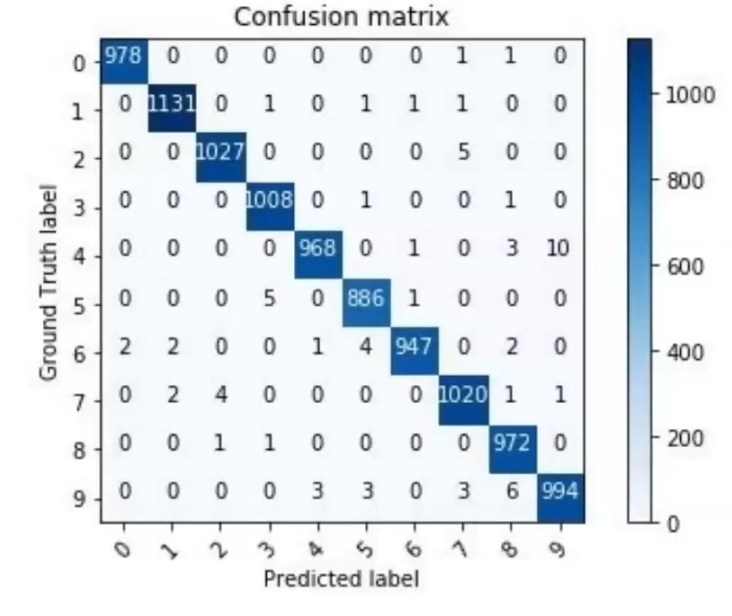
En el caso de la clasificación multiclase para esta métrica, podemos calcular la matriz de confusión igualmente, solo que en vez de 0 y 1, va a ser una variable al cuadrado de n x n.
¿Qué sigue?
Para que cumplas tus sueños y sigas aprendiendo sobre el mundo tecnológico, que ofrece excelentes oportunidades para desarrolladores y aspirantes a data scientist, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp. En esta formación intensiva adquirirás todos los conocimientos teóricos y prácticos imprescindibles para que sigas tu camino hacia el éxito. ¡No esperes más para obtener lo que quieres y solicita información ahora!











