Mínimos cuadrados en forma matricial

Los mínimos cuadrados son valores que nos ayudan a elegir valores de w que minimizan la suma de errores al cuadrado. En este artículo, veremos cómo se manejan los mínimos cuadrados en forma matricial.

Mínimos cuadrados en forma matricial

Existen dos formas para la ecuación:

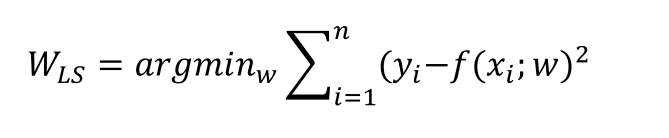
Si desarrollamos dicha fórmula podemos llegar a la ecuación de mínimos cuadrados en forma matricial:

X^T XW’ = X^T y

O lo que es lo mismo:

W’ = (X^T X)^-1 X^T y

Donde la matriz X viene definida como:

Se le añade un 1 a cada fila de la matriz por convención y por la componente w₀ de la ecuación — Indicado por R^d+1

¿Por qué n > d?

La expresión n > d indica que el número de observaciones debe ser mayor que el número de dimensiones. Veamos un ejemplo para entenderlo mejor:

#Mínimos cuadrados en forma matricial
import pandas as pd

data = [['Teresa', 8.7, 7], ['Alex',m 6.7, 8], ['Sara', 9, 9.1], ['Pepe', 7, 5.1]]
df

	Name	Media bachiller – Grade	Media selectividad – Test
0	Teresa	8.7	7.0
1	Alex	6.7	8.0
2	Sara	9.0	9.1
3	Pepe	7.0	5.1

El número n es el número de observaciones y el número d son las dimensiones. Es decir, si en nuestro problema tenemos 3 personas a estudiar y vamos a analizar la influencia de media de bachiller y de su media en selectividad, tendremos que:

• Número de observaciones n: personas.
• Número de dimensiones d: variables (Media bachiller, Media selectividad).

	Name	Media bachiller – Grade	Media selectividad – Test
0	Teresa	8.7	7.0
1	Alex	6.7	8.0
2	Sara	9.0	9.1
3	Pepe	7.0	5.1

En el caso de que n < d + 1 no podríamos aplicar mínimos cuadrados en forma matricial, ya que (X^T X)^-1 no existiría y habría un número infinito de soluciones.

Ejercicio sobre mínimos cuadrados en forma matricial

Calcula (X^T X)^-1:

Primero importaremos la librería Numpy:

#Mínimos cuadrados en forma matricial
import numpy as np

x = np.array ([[1,  8.7,  7],
                         [1,  6.7,  8],
                         [1,  9,  9.1],
                         [1,  7,  5.1]])

print (X)

[[1, 8.7, 7],

[1, 6.7, 8],

[1, 9, 9.1],

[1, 7, 5.1]]

#Mínimos cuadrados en forma matricial
X_Y = np.transpose (X)
X_t

array (

[[1. , 1. , 1. , 1.],

[8.7 , 6.7 , 9. , 7.],

[7. , 8. , 9.1 , 5.1]])

#Mínimos cuadrados en forma matricial
prod = np.dot (X_t, X)

inv_prod = np.linalg.inv (prod)
print (inv_prod)

[[15.79028203 -1.73113364 -0.26724424]

[-1.73113364 0.31926267 -0.10617512]

[-0.26724424 -0.10617512 0.150783641]]

Calcula (X^T X)^-1

#Mínimos cuadrados en forma matricial
import numpy as np

x = np.array ([[1,  8.7,  7],
                         [1,  6.7,  8]])

print (X)

[[1, 8.7, 7],

[1, 6.7, 8]

#Mínimos cuadrados en forma matricial
X_Y = np.transpose (X)
X_t

array (

[[1. , 1.],

[8.7 , 6.7]])

#Mínimos cuadrados en forma matricial
prod = np.dot (X_t, X)
print (prod)

[[2. 15.4 16.]

[15.4 120.58 123.2]

[16. 123.2 128. ]]

Si intentamos calcular la inversa de esto…

#Mínimos cuadrados en forma matricial
inv_prod = np.linalg.inv (prod)
print (inv_prod)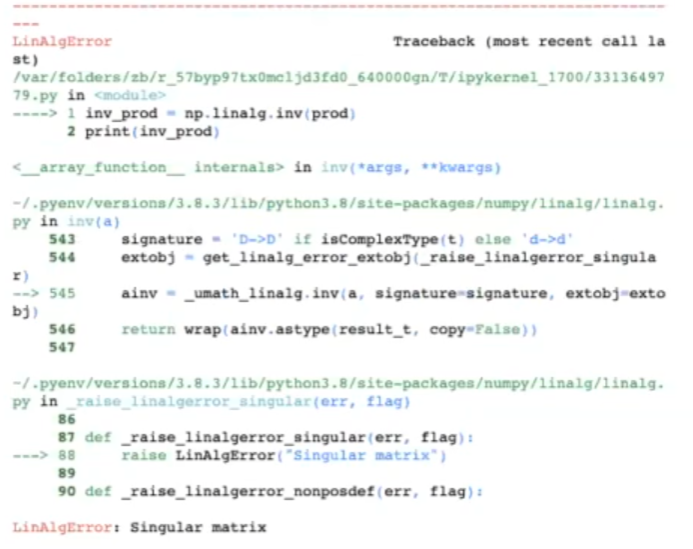

Nos da un error, ya que dice que es una matriz singular. Eso sucede porque el número de filas es menor que el número de columnas.

La filosofía detrás de los mínimos cuadrados

¿Recuerdas cómo funcionan los sistemas de ecuaciones?

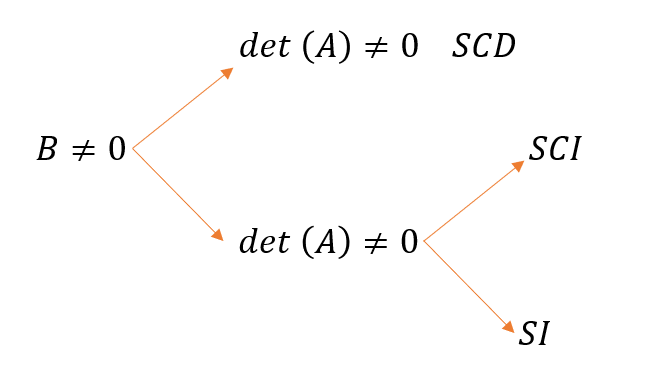
Cuando un sistema es incompatible significa que tiene infinitas soluciones, pero hay una forma de encontrar una solución aproximada y aquí es donde entran en juego los mínimos cuadrados.

Supongamos que tratamos de resolver un sistema de la forma Ax = b y que no existe solución para este sistema. En este caso, puede ser interesante estudiar para qué vector o vectores x’, Ax ≈ b, tratamos de buscar una solución aproximada del sistema.

Una forma de interpretar esta aproximación es la siguiente: si Ax ≈ b, entonces podemos intentar encontrar x, tal que kAx – bk sea lo menor posible. Es decir, tratamos de resolver el problema minx ||Ax – b||.

Si el sistema tiene solución, el mínimo del problema anterior es cero, y, por tanto, Ax = b; pero si no hay solución, tiene sentido buscar el vector x que haga menor esa norma y, por tanto, que más se parece a una solución.

Al final, al igual que hemos hecho antes, desarrollamos dicha expresión, se llega a la conclusión de que se trata de resolver el sisterna:

A^T Ax’ = A^T b

¿Cómo avanzar?

Para poder acceder a mejores opciones laborales, tenemos para ti el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación en la que adquirirás todos los conocimientos que te permitirán obtener el trabajo de tus sueños en pocos meses. ¡No esperes más para impulsar tu carrera y solicita información ahora!