¿Cómo obtener una matriz original sin perder información?

Dada una matriz de componentes principales, podemos obtener una matriz original sin perder información de ningún tipo si multiplicamos por la inversa de la matriz de autovectores. En este post, detallamos el proceso.

Obtener una matriz original

En un ejercicio anterior estuvimos trabajando en un algoritmo Eigenfaces que determina si una imagen dada pertenece a la cara de George Bush o no.

En ese artículo, haremos el proceso de obtener la matriz original de una imagen que previamente había sido transformada, transformando de vuelta al dominio de la imagen o imágenes mismas.

La matriz de autovectores es una matriz ortonormal. Eso significa que la transpuesta es su propia inversa ya que:

V x VT = 1

Así pues:

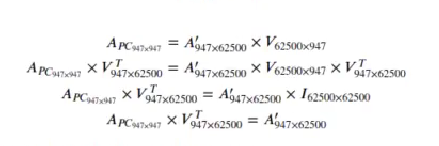
Es decir, el vector que contiene la imagen original normalizada se puede obtener como:

A¹ = A_PC x V^T

Después, desnormalizamos A¹ para volver al vector original de la imagen:

A_ij = (A’_ij + μ_j) . σ_j + μ_j

Vamos a recuperar una imagen y a obtener una matriz original. Cogemos la imagen de PCA, le aplicamos la transformación y luego lo único que haremos es multiplicar esto por la matriz de rotación traspuesta, lo multiplicamos por la desviación típica y le sumamos la media:

#Obtener una matriz original
recover_pic <- (pic_pca %*% t (pr_pics$rotation)) * pr_pics$scale + pr_pics$center
summary (array (recover_pic))
#El valor de un píxel siempre está entre e y 1, los errores en el redondeo hacen que a veces esto no se cumpla.
recover_pic [recover_pic < 0] <- 0
recover_pic [recover_pic > 1] <- 1
dim (recover_pic)

En ocasiones, por cuestiones de redondeo, cuando estamos trabajando con valores muy grandes, podemos encontrarnos con que tenemos un valor negativo muy pequeño o un valor mayor de 1, lo cual no debería suceder. El recover_pic evita que esto suceda.

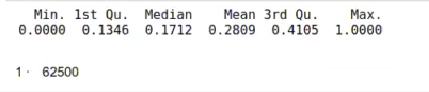
En este proceso se producen errores de redondeo. Es por eso que deben ajustarse y limitar el rango de la imagen a [0,1]. La codificación de los números en binario se hace siguiendo el estándar IEEE 754.

#Obtener una matriz original
bin2dec <- function (binaryvector) {
sum (2 ^ (which (rev (binaryvector)) - 1))
}
fracbin2dec <- function (frac) {
sum (2 ^ (-which (frac)))
} 
xp <- c (F, T, T, T, T, T, F, F)
frac <- c (F, T, F, F, F, F, F, F, F, F, F, F, F, F, F, F, F, F, F, F, F, F, F)
2 ^ (bin2dec (xp) - 127) * (1 + fracbin2dec (frac))

0.15625

Para ver la imagen reconvertida solo tenemos que hacer un plot_row_Image:

#Comprobamos que hemos podido recuperar la imagen original
plot_row_image (recover_pic)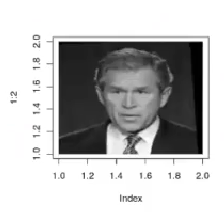

Hemos visto cómo recuperar una matriz original sin perder ningún tipo de información y evitando, en la medida de lo posible, errores que puedan afectar los resultados.

Si quieres seguir aprendiendo sobre estas temáticas, puedes inscribirte en nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que adquirirás de manera rápida y eficaz todos los conocimientos necesarios para incursionar en un mercado laboral lleno de oportunidades y puedas seguir forjando tu futuro exitoso.

¡Anímate a cambiar tu vida y solicita más información!