En este post vamos a realizar un ejercicio de preprocesado en R aplicando regresión lineal.
Vamos a hacer una predicción de la potencia de generación de una central de ciclo combinado con un modelo de regresión lineal.
Contexto previo al ejercicio de preprocesado en R
El conjunto de datos contiene 9568 puntos de datos recopilados de una Central de Ciclo Combinado durante 6 años (2006-2011), cuando la planta de energía se puso a funcionar con carga completa. Las características consisten en variables continuas ambientales promedio por hora, temperatura (T), presión ambiente (AP), humedad relativa (HR) y vacío de escape (V) para predecir la producción neta de energía eléctrica por hora (EP) de la planta, relacionadas linealmente.
Las características consisten en variables ambientales promedio por hora.
- Temperatura (AT) en el rango de 1.81 C y 37.11 «C.
- Presión ambiental (AP) en el rango de 992.89-1033.30 milibares.
- Humedad relativa (HR) en el rango de 25.56% a 100.16%.
- Vacío de escape (V) en el rango de 25.36-81.56 cm Hg.
- Producción neta de energía eléctrica por hora (EP) 420.26-495.76 MW.
Los promedios se toman de varios sensores ubicados alrededor de la planta que registran las variables ambientales cada segundo. Las variables se dan sin normalización.
Cada variable viene uno un rango de funcionamiento diferente y es difícil compararlos entre ellos.
¿Qué es el preprocesado?
El preprocesado es una fase característica de distintos lenguajes de programación, que consiste en leer el código fuente antes de la compilación y hacerlo más legible para el ordenador para ese siguiente paso, el de compilación.
Este proceso no consiste en convertir el lenguaje de alto nivel en lenguaje de máquina, ya que esto es lo que hace el proceso de compilación.
El ejercicio de preprocesado en R aplicando regresión lineal es, como su nombre indica, un paso que se lleva a cabo antes del procesado de datos y sirve como modelo de referencia.
Desarrollo del ejercicio de preprocesado en R aplicando regresión lineal
In [ ] : powerplant <- read.csv ("data/powerplant.csv")
In [ ]: idx <- sample (1:nrow (powerplant), nrow(powerplant) * 0.7)
powerplant.train <- powerplant [idx, ]
powerplant.test <- powerplant [-idx, ]
In [ ] : library (GGally)
options (repr.plot.height = 4, repr.plot.width = 6)
ggpairs (powerplant.train,
lower = list (continuous = wrap ("density", alpha = 0.8, size =0.2, color = 'blue'))
#lower = list (continuous = wrap ("points", alpha= 0.3, size-0.1, color = 'blue'))
)Registered S3 method overwritten by ‘GGally’:
method from
+.gg ggplot2
In [25] : set.seed (1234)
model_powerplant <- lm (PE ~., data = powerplant.train)
summary (model_powerplant)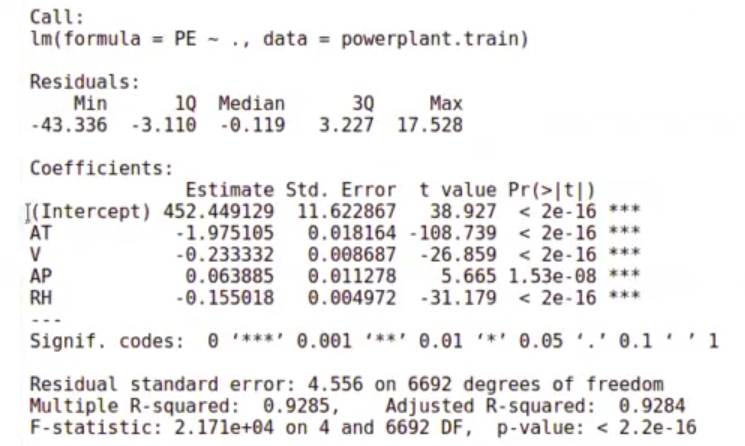
In [26] : powerplant.test$pe_est <- predict (model_powerplant, powerplant.test)
paste ("Error cuadrático medio ", sqrt (mean ((powerplant.test$pe - powerplant.test$pe_est) ^ 2)))‘Error cuadrático medio 4.56403549677779’
In [28] : caret :: postResample (powerplant.test$PE, powerplant.test$pe_est)RMSE: 4.56403549677779
Rsquared: 0.929241932851849
MAE: 3.65343848377682
Podemos escalar nuestros datos para que todos estén en el mismo rango y calcular mejor la varianza de error.
Habría que hacerlo solo con los elementos de train, porque se supone que los datos de test no los hemos visto nunca.
In [30]: library(dplyr)
preProcValues <- powerplant.train %>% select (-PE) %>% caret :: preProcess (method = c("center", "scale"))
powerplant_norm.train <- predict (preProcValues, powerplant.train) summary (powerplant_norm.train)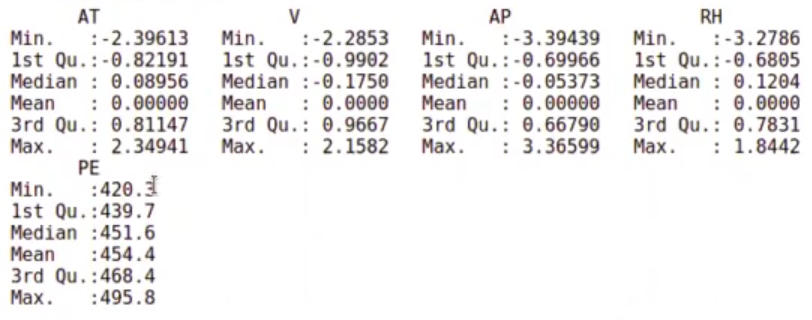
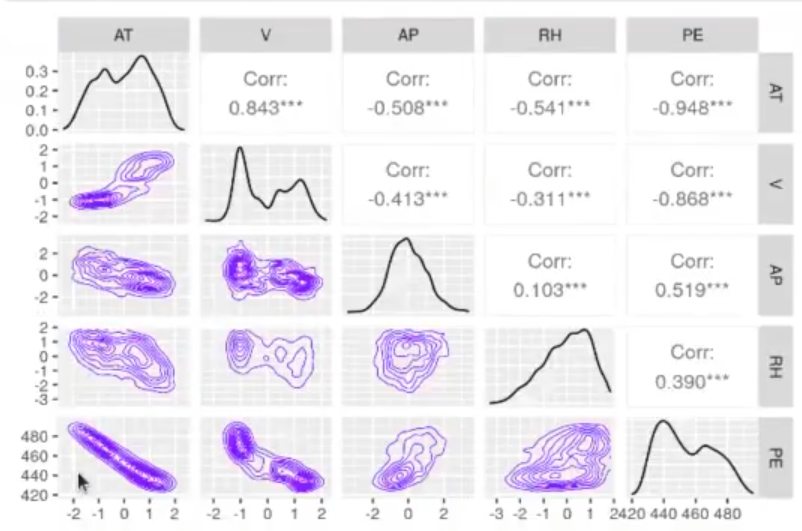
In [ ]: ggpairs (powerplant_norm.train, lower = list (continuous = wrap ("density", alpha = 0.8, size-0.2, color = "blue'))
)
Realizamos el modelo de regresión lineal:
In [39] : model_powerplant_norm <-lm (PE ~., data = powerplant_norm.train)
summary (model_powerplant_norm)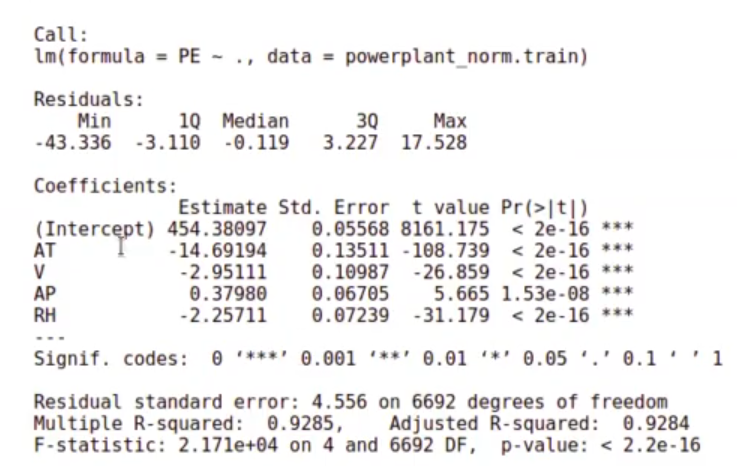
Para seguir con el preprocesado en R aplicando regresión lineal, vamos a realizar el train:
In [46] : powerplant_norm.train$pe_est < -predict (model_powerplant_norm, powerplant_norm.train)
paste ("Error cuadrático medio", sqrt (mean ((powerplant_norm.train$PE-powerplant_norm.train$pe est) ^ 2)))‘Error cuadrático medio 4.55454947491387’
In [41]: powerplant_norm.train <- predict (preProcValues, powerplant_norm.train)
summary (powerplant_norm.train)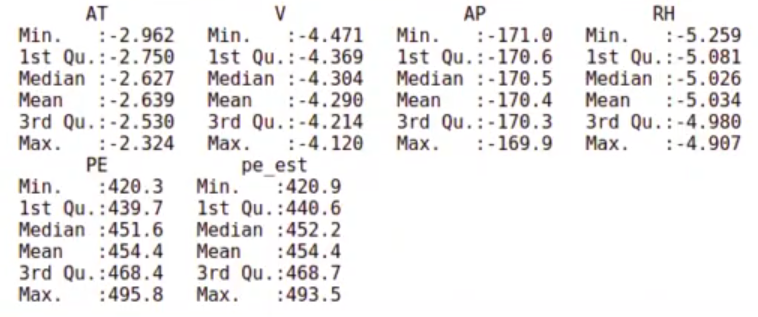
In [ ] : powerplant_norm.test <- predict (preProcValues, powerplant.test)
powerplant_norm.test$pe_est <- predict (model_powerplant_norm, powerplant_norm.test)
paste ("Error cuadrático medio", sqrt (mean ((powerplant_norm.test$PE-powerplant_norm.test$pe_est) ^ 2)))El siguiente paso en el ejercicio de preprocesado en R aplicando regresión lineal es realizar el testing:
In [44] : summary (powerplant.test)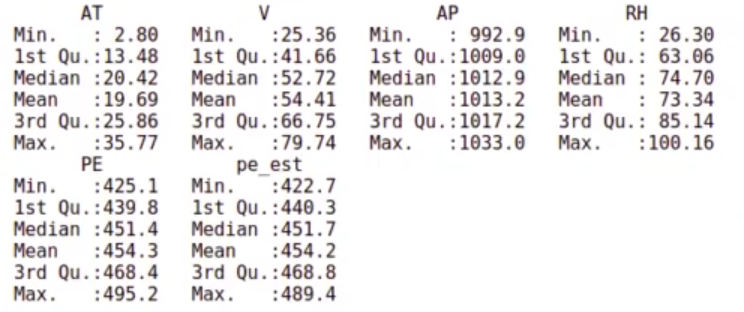
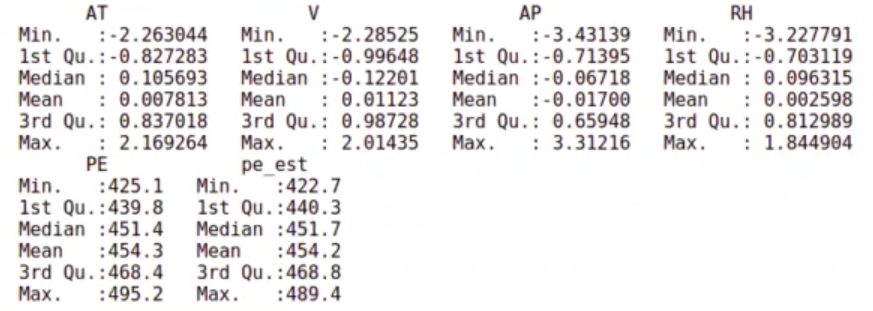
Y con esto ya tenemos completo nuestro ejercicio de preprocesado en R aplicando regresión lineal.
Seguro que tendrás dudas después de haber visto de manera práctica cómo funciona el preprocesado en R aplicando regresión lineal. ¡No te preocupes! En Keepcoding tenemos la respuesta a todas tus preguntas. Gracias a nuestro Bootcamp Data Science y Big Data podrás entender toda la conceptualización y teorías necesarias para dominar, en pocos meses, este amplio mundo.
Al terminar esta formación intensiva tendrá la oportunidad de conseguir tu primer empleo en uno de los mercados más prolíficos en la actualidad y convertirte en un gran profesional.
¡Sigue persiguiendo tus sueños y pide más información!











