¿Qué es y cómo factorizar una diferencia de cuadrados perfectos?

La diferencia de cuadrados perfectos es un concepto muy usado en matemáticas. Sirve para entender el álgebra, pero también para resolver operaciones avanzadas en otras áreas e inclusive nos puede servir para entender cómo funcionan muchas áreas de la programación.

El día de hoy, en este artículo, queremos mostrarte qué es la diferencia de cuadrados perfectos y cómo puedes factorizarla.

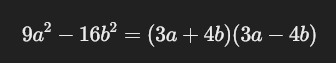
¿Qué es la diferencia de cuadrados perfectos?

La diferencia de cuadrados perfectos es una expresión algebraica que sigue este formato:

a^2 – b^2

Donde tanto a como b son términos que pueden ser números, variables o incluso expresiones más complejas, siempre y cuando estén elevados al cuadrado. La clave está en la palabra “diferencia”, ya que indica que hay una resta entre dos cuadrados perfectos.

La fórmula que usamos para factorizar una diferencia de cuadrados perfectos es muy sencilla y sigue esta estructura:

a^2 – b^2 = (a + b)(a – b)

Lo que estamos haciendo aquí es descomponer la diferencia en un producto de dos binomios. Uno de los binomios tiene una suma y el otro una resta. A estos binomios se les llama binomios conjugados.

¿Cómo factorizar una diferencia de cuadrados perfectos?

Factorizar una diferencia de cuadrados perfectos es un proceso directo si sigues estos pasos:

Paso 1: Identificar si es una diferencia de cuadrados

Antes de empezar a factorizar, es importante verificar que la expresión realmente sea una diferencia de cuadrados. Para que una expresión cumpla con esto, debe:

• Ser un binomio (dos términos).
• Ambos términos deben tener raíces cuadradas exactas.
• Los términos deben estar separados por una resta.

Por ejemplo:

25x^2 – 121

Cumple con todas las condiciones. Ahora estamos listos para factorizar.

Paso 2: Calcular las raíces cuadradas

Calcula la raíz cuadrada de ambos términos. En el ejemplo anterior:

• La raíz cuadrada de 25x^2 es 5x.
• La raíz cuadrada de 121 es 11.

Paso 3: Crear los binomios conjugados

Con las raíces calculadas, escribimos dos binomios conjugados. Uno tendrá una suma y el otro una resta:

25x^2 – 121 = (5x + 11)(5x – 11)

¡Listo! Hemos factorizado la expresión utilizando la diferencia de cuadrados perfectos.

Aplicaciones de la diferencia de cuadrados perfectos

La factorización por diferencia de cuadrados perfectos tiene aplicaciones más allá del simple álgebra. En problemas de geometría, física, e incluso en optimización de algoritmos en programación, este método es increíblemente útil.

• En álgebra: La factorización de cuadrados perfectos permite simplificar ecuaciones cuadráticas y resolver problemas de manera más eficiente. También es una técnica clave cuando se trabaja con identidades algebraicas más avanzadas.
• En geometría: En ciertos problemas de geometría, como el cálculo de áreas y volúmenes, la diferencia de cuadrados puede ayudar a simplificar las ecuaciones para obtener soluciones rápidas y precisas.

¿Por qué aprender a factorizar diferencias de cuadrados perfectos?

Saber cómo factorizar la diferencia de cuadrados perfectos no solo te ayudará en las matemáticas, sino que es una habilidad fundamental para muchos otros campos, como la programación y la ciencia de datos. A medida que resuelves problemas, verás cómo este concepto puede hacer que tu trabajo sea mucho más eficiente.

Además, aprender este tipo de técnicas te prepara para enfrentar desafíos más complejos en matemáticas y ciencias aplicadas. Y si decides adentrarte en el mundo del desarrollo de software o la ciencia de datos, te darás cuenta de que este tipo de habilidades son esenciales para resolver problemas más grandes y significativos.

Si te ha interesado este post y quieres seguir aprendiendo, puedes hacerlo por medio de nuestro bootcamp en programación desde cero. Con este te enseñaremos a aplicar diferentes conceptos relacionados con las matemáticas y la programación, lo cual te abrirá las puertas a un sector en constante crecimiento y con alta demanda. ¡Únete a nosotros y vive una experiencia única!