El término espacio nulo de una matriz es un término particularmente relacionado con la independencia lineal de vectores. El espacio nulo de una matriz A, expresado como N(A), consiste en todas las soluciones a la ecuación Ax = 0.
Una solución inmediata a esta ecuación es x = 0, que establece la independencia lineal. Esta solución va a ser la única que exista para los casos de matrices invertibles. En el caso de las matrices singulares (aquellas que no son invertibles, que tienen determinante igual a cero), van a existir soluciones que no son cero para la ecuación Ax= 0. El conjunto de todas estas soluciones va a representar el espacio nulo de una matriz.
Ejercicio sobre el espacio nulo de una matriz
El espacio nulo es simplemente calcular la solución de la ecuación a por x igual a cero (AX = 0).
Veamos cómo funciona el espacio nulo de una matriz por medio de un ejercicio de aplicación. Vamos a encontrar el espacio nulo para la siguiente matriz:
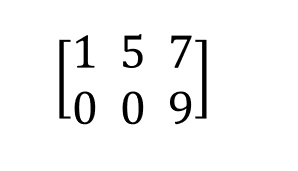
Lo primero que debemos hacer es definir la matriz en sympy:
#Ejercicio sobre el espacio nulo de una matriz
A = sp.Matrix (((1, 5, 7), (0, 0, 9)))
print (A)Matrix ([[1, 5, 7], [0, 0, 9]])
Calcular el espacio nulo es tan sencillo como usar nullspace, es decir, es simplemente despejar la x.
Como ya habrás podido observar, calcular el espacio nulo de una matriz está íntimamente relacionado con la dependencia e independencia lineal. Por tanto, lo que nos está pidiendo la ecuación es que le brindemos los valores que resuelven la siguiente ecuación: α1 [1.2, 1.1] + α2 [-2.2, 1.4] = 0, cuyo resultado es igual a cero.
Entonces, si usamos la función nullspace, que viene definida dentro de sympy, nos imprime el resultado:
# rango y nulidad de una matriz
#Ejercicio sobre el espacio nulo de una matriz
#Estamos buscando todos los valores de x que hacen esta ecuación AX = 0
x = A.nullspace ()
x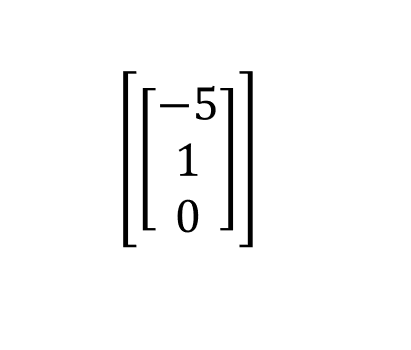
Nos dice que ese resultado es -5, 1 y 0. Esto quiere decir que los valores de x que hacen 0 a la ecuación —en este caso es una matriz, pero funciona exactamente del mismo modo (recordemos que también se puede escribir una matriz en forma de ecuación)—, el espacio nulo de una matriz 1 5 7 0 0 9 es -5 1 0. Simplemente estamos calculando todos los valores de x que hacen 0 a esa ecuación.
¿Es correcto? Vamos a comprobarlo. Para ello, hacemos una prueba que consiste en confirmar si, al multiplicar la matriz a por x y usar la x que nos ha dado como resultado el ejercicio anterior (o sea -5, 1, 0), nos debería dar un número igual a 0.
Vamos, pues, a definir el resultado que nos han dado aquí, es decir, -5, 1 y 0.
# calcular espacio nulo de una matriz
#Ejercicio sobre el espacio nulo de una matriz
A = np.array ([[1, 5, 7],
[0, 0, 9]])
x = np.array ([[-5], [1], [0]])
print (A.shape)
print (x.shape)(2, 3)
(3, 1)
Ahora, si multiplicamos el resultado usando la función .dot en numpy, que nos permite multiplicar matrices, el resultado que nos da es el que nos debería dar, es decir, cero:
#Ejercicio sobre el espacio nulo de una matriz
A.dot (x)array ([[0],
[0]])
El resultado que nos ha dado el nullspace es correcto. Son estos los valores de x que hacen que la ecuación sea igual a 0.
Como hemos visto, tiene mucha relación con la dependencia e independencia lineal.
Nullspace de sympy
El nullspace de sympy es una función que sirve para encontrar el espacio nulo de una matriz. Cuando usamos nullspace, lo que se devuelve es una lista de vectores columna que abarcan el espacio nulo de una matriz.
El espacio nulo de una matriz está denotado por la siguiente ecuación:
NA ={X ∈ Rn : Ax = 0} = espacio nulo de la matriz A o nul a
¿Quieres seguir aprendiendo?
Gracias a este ejercicio sobre el espacio nulo de una matriz estás más cerca de dominar el Big Data. Si te gustaría acceder a una de las disciplinas más demandadas y mejor pagadas del mercado laboral actual, no te pierdas el Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, con el que seguirás progresando en este ámbito para, en pocos meses, ser un experto dentro del mundo IT. ¡Entra ya para solicitar información y anímate a cambiar tu futuro!











