Si has hecho machine learning es muy probable que te hayas encontrado con unos cuantos problemas de overfitting.
Imagina que estás haciendo un ejercicio de machine learning; estás evaluando un modelo de aprendizaje automático para encontrar un punto óptimo donde puedas acomodar tu conjunto de datos y obtener un modelo entrenado. En un punto del camino te das cuenta de que tu conjunto de datos de entrenamiento está creando un desbalance, debido a que has introducido muchísimos datos en el inicio del train y se han producido problemas de overfitting.
Los problemas de overfitting o sobreajuste se dan cuando una función está demasiado alineada con un conjunto limitado de puntos de datos. Esto causa que el modelo solo sea útil con el dataset de entrenamiento (el conjunto inicial de datos), pero en el momento en el que le introduzcamos datos nuevos, nuestro modelo va a explotar y va a generar un montón de ruido, porque no sabe qué hacer con los datos que hemos ingresado.
Regresión lineal en problemas de overfitting
Una variable
La regresión lineal en problemas de overfitting se usa para minimizar este obstáculo. Lo que se hace es poner una restricción a la solución que tengamos.
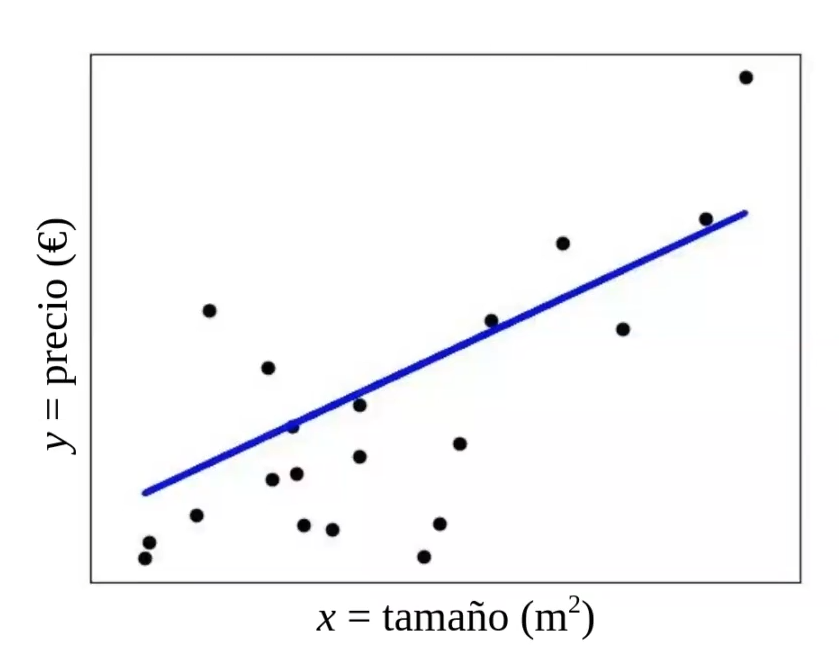
Tenemos, por tanto, una regresión lineal de una variable, que es una recta:

Tenemos la función de coste y lo que queremos es minimizar esta función, que en este caso son los mínimos cuadrados y el error cuadrático medio o MSE. Utilizamos el método que sea de nuestra preferencia para minimizar la función de coste, puede ser descenso por gradientes o cualquier otra.
Varias variables
Si necesitamos resolver problemas de overfitting usando regresión lineal con varias variables, realizaremos el mismo proceso que con una sola variable, aunque con unas pequeñas modificaciones. En vez de tener un solo coeficiente, el ω1, lo que vamos a tener es n coeficientes con n número de variables.
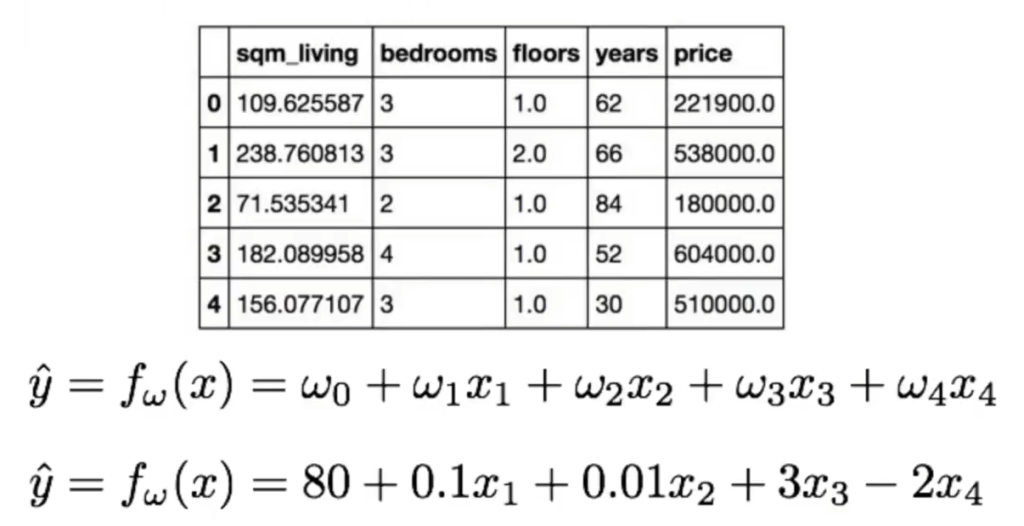
Hay que tener muchísimo cuidado con la interpretación de estos coeficientes en problemas de overfitting, ya que si hay una variable negativa es porque el coeficiente afecta negativamente.
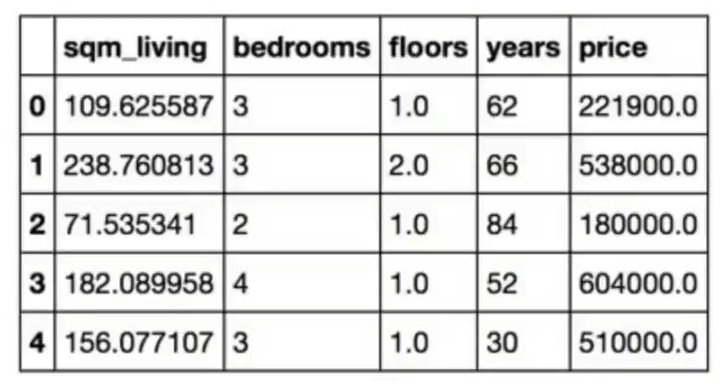
En el caso de la imagen, tenemos cuatro características (sqm_living, bedrooms, floors y years), que corresponden a los cuatro coeficientes de la función (ω1x1, ω2x2, ω3x3 y ω4x4) y tenemos una variable objetivo, que es el precio (price).
El vector x tiene cuatro valores, que corresponden a los 4 coeficientes (características). El vector y tiene 1 valor, que corresponde al precio.
Este es un ejemplo real y vemos que 2×4 es negativo; este valor corresponde a los años de la casa (years). Esto significa que, a medida que la casa tiene más años, el precio baja.
Como ya hemos dicho, hay que tener muchísimo cuidado con la interpretación, porque tenemos los valores de 0.1x1 y 0.01x2, con lo que podríamos decir que 0.1 es 10 veces más grande que 0.01, pero no funciona así. 0.1 es más importante que 0.01, tiene más peso, pero no necesariamente es 10 veces más importante, porque no sabemos cuál es la magnitud de x1 y tampoco sabemos cuál es la magnitud de x2.
En este caso, sabemos que x1 es el número de habitaciones (bedrooms) y x2 es el número de pisos (floors). Probablemente la media del número de pisos sea menor que la media del número de habitaciones (que está más o menos por 3), pero no podemos estar seguros.
Ahora, veamos la forma matricial de la regresión lineal en problemas de overfitting:
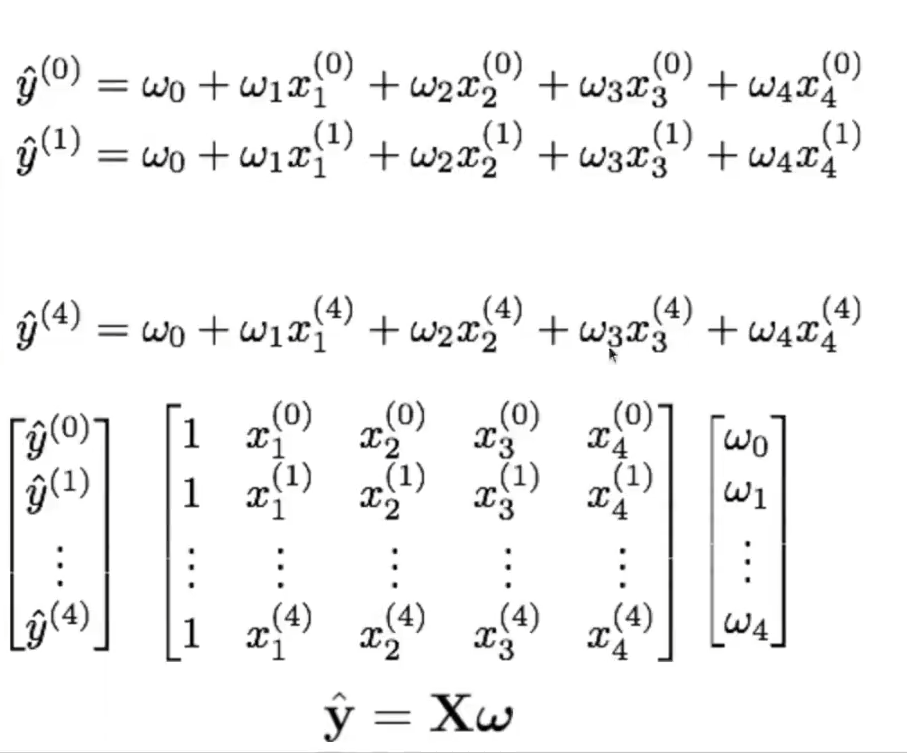
- La solución al problema de optimización anterior tiene una expresión analítica cerrada:
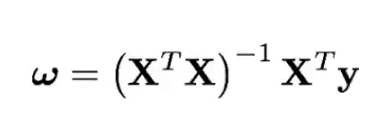
- ¿Qué pasa si XTX no es invertible? La solución no es única, debido a:
- Variables redundantes (linealmente dependientes).
- Más variables/características que muestra.
- Consecuencias:
- Inestabilidad de la solución (overfitting).
- Coeficientes del modelo contraintuitivos.
Problemas del overfitting
Lo que acabamos de ver se puede resumir así:
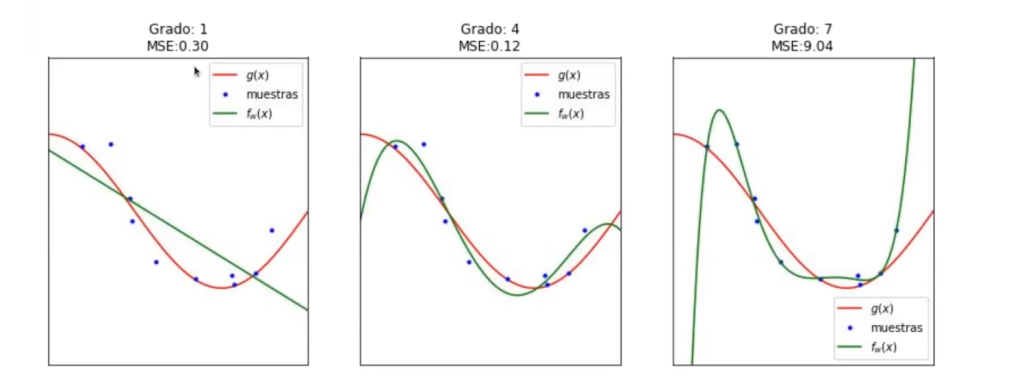

Con esto, damos por terminada la relación entre la regresión lineal y los problemas de overfitting.
¿Qué sigue?
En el proceso de aprender y hacer machine learning nos podemos encontrar con muchos inconvenientes, entre ellos los problemas de overfitting. Por eso es importante mantener buenas prácticas de machine learning, las cuales puedes adquirir a través de nuestro Big Data, Inteligencia Artificial & Machine Learning Full Stack Bootcamp, una formación intensiva en la que aprenderás todo lo necesario relacionado con este ámbito para triunfar en el mercado laboral. ¡Anímate a impulsar tu futuro y solicita más información ahora!











